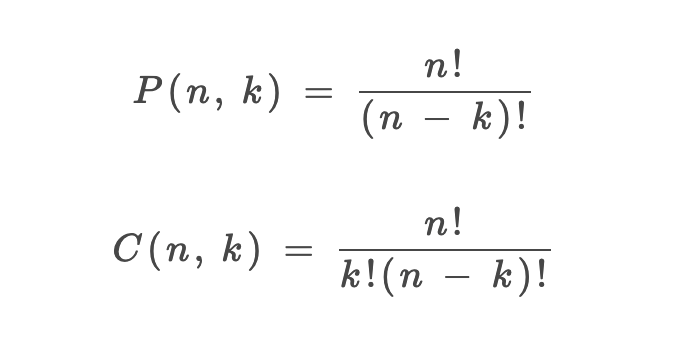Transformer 中的 position embedding 的设计
前言
Transformer 使用 Attention 结构来进行建模,在 NLP 和 CV 领域都有比较好的效果,其主要结构如下:
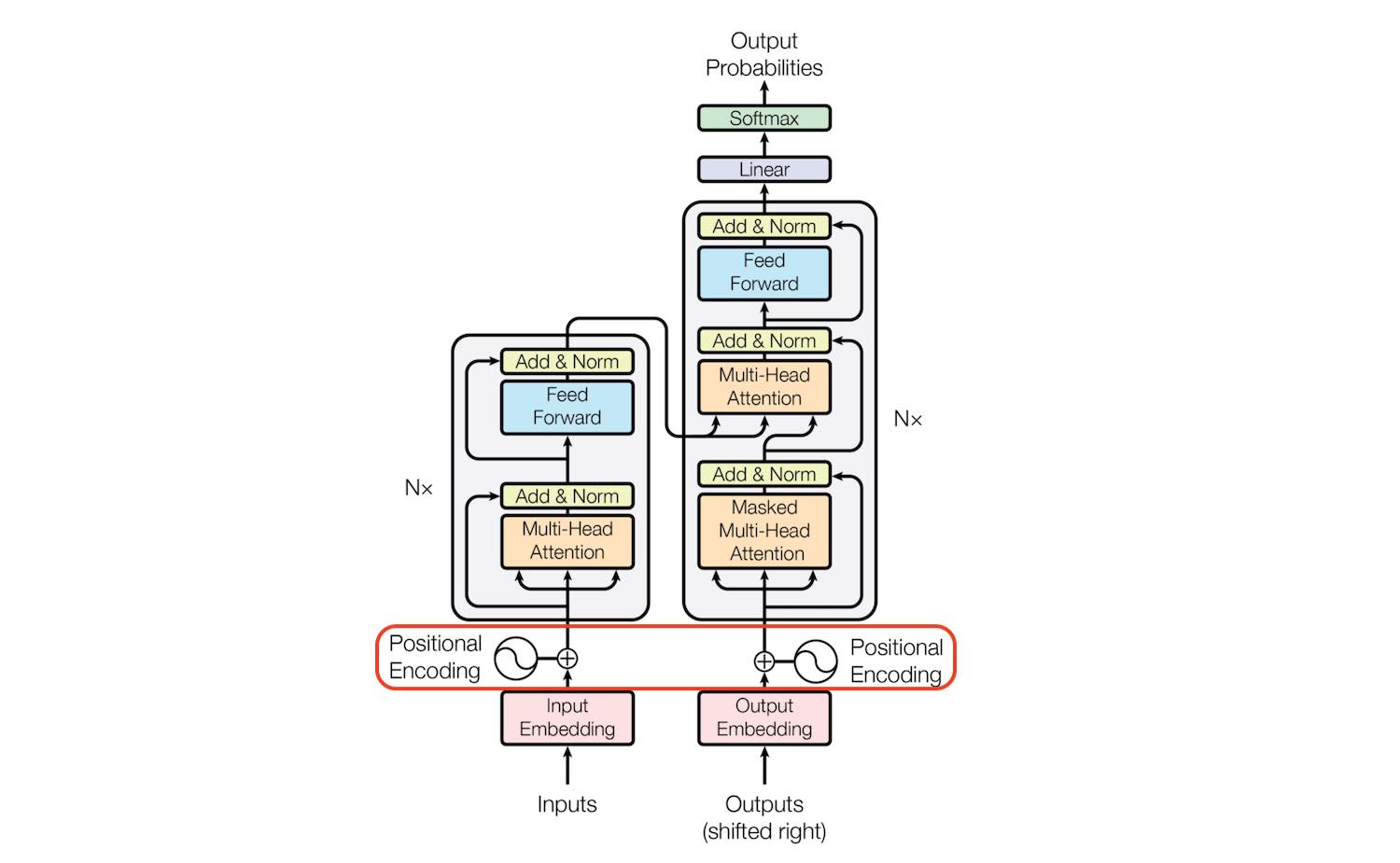
如果只取左边的部分,则退化为 BERT 类结构。 如果只取右边部分,则变成 GPT 类结构。
Transformer 使用 Attention 结构来进行建模,在 NLP 和 CV 领域都有比较好的效果,其主要结构如下:

如果只取左边的部分,则退化为 BERT 类结构。 如果只取右边部分,则变成 GPT 类结构。
标题、时间、会议、领域、code、paper 链接
题目:Targeted Supervised Contrastive Learning for Long-Tailed Recognition
来源:CVPR 2022
xuejiao 阿姨,展信佳:
有很多话想说,但是又不知道怎么说出口。在微信上打了很多,但感觉似乎很容易被忘掉,所以想来想去,还是写一封信,将现在的这些想法都记录下来。过很多年后回忆起来,就还能感受到自己的鲜活!
Github:https://github.com/openai/gpt-2 、https://github.com/openai/gpt-3
GPT 系列是历史非常悠久的论文了,gpt1 甚至在 bert 之前就发布了。 但在下游任务上的表现,并没有 bert 亮眼,所以一直默默无闻。最近 chatgpt 大火,又把 gpt 的论文翻出来复习一下。
分割类问题也算是动态规划的常客。对于字符类问题,状态转移方式往往依赖于相邻的位置。
0-1背包问题,状态方程不仅依赖于相邻的位置,还依赖于满足条件的空间位置。
对于分割类型题,动态规划的状态转移方程通常并不依赖相邻的位置,而是依赖于满足分割条件的位置。
股票买卖类问题的「状态」有三个,第一个是天数,第二个是允许交易的最大次数,第三个是当前的持有状态(即之前说的 rest 的状态,我们不妨用 1 表示持有,0 表示没有持有)。然后我们用一个三维数组就可以装下这几种状态的全部组合:
1 | dp[i][k][0 or 1] |
背包问题主要分为三种:
W 的背包和 N 个物品,每个物品有重量和价值两个属性。其中第 i 个物品的重量为 wt[i],价值为 val[i],现在让你用这个背包装物品,最多能装的价值是多少?sum / 2 的背包和 N 个物品,每个物品的重量为 nums[i]。现在让你装物品,是否存在一种装法,能够恰好将背包装满?根据 Leetcode 的习惯,子序列(subsequence)不必连续,子数组(subarray)或子字符串(substring)必须连续。
动态规划中,子串子序列的问题大概分为如下几种:
单条数组(字符)内部的对比,比如:
两条数组(字符)之间做对比,比如
组合、排列、子集是 leetcode 中比较常见的题目系列,主要区别在于:
| 名称 | 概念 | 示例题目 |
|---|---|---|
| 排列 | 每项结果有序,即[1,2] 与 [2,1]是两个结果 | 46. 全排列、47. 全排列 II、 |
| 组合 | 每项结果无序,即[1,2]与[2,1]是一个结果 | 39. 组合总和、216. 组合总和 III、40. 组合总和 II、77. 组合 |
| 子集 | 与组合类似,但会有额外的限制,比如数量等 | 78. 子集、90. 子集 II |