动态规划-子串子序列类型

定义

根据 Leetcode 的习惯，子序列（subsequence）不必连续，子数组（subarray）或子字符串（substring）必须连续。

动态规划中，子串子序列的问题大概分为如下几种：

• 单条数组(字符)内部的对比，比如:

  • 5. 最长回文子串 + 516. 最长回文子序列
  • 300. 最长递增子序列 + 674. 最长连续递增序列（不使用动态规划反而更简单一些）

• 两条数组(字符)之间做对比，比如

  • 1143. 最长公共子序列 和 最长公共子串 (leetcode 上没有这个题，随便找了一个)
  • 72. 编辑距离

以下将分别举例分析

最长回文系列

dp 的定义为 字符串s的下表范围 [i:j] 中的最长回文子序列&串的长度是 dp[i][j]

题目 516. 最长回文子序列

题目部分

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

输入：s = “bbbab”
输出：4
解释：一个可能的最长回文子序列为 “bbbb”

解法

dp[i][j] 表示字符串s的下标范围 [i,j] 内最长回文子序列的长度

1、 i == j，任何长度为 1 的字符串都是回文序列，此时 dp[i] 均为 1，也就是对角线蓝色的部分；

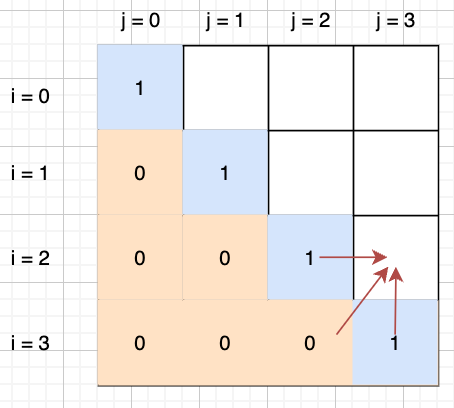
2、因为 i 是左边界， j 是右边界，不存在 i > j 的字符串，也就对下三角橙黄色的部分，均为0；

3、如果 s[i] == s[j]， 那么可以在内部 dp[i+1][j-1]最长子序列的基础上，增加 2 ，即 dp[i][j] = dp[i+1][j-1] + 2

4、否则，取当前[i,j]的子区间[i+1,j]和[i,j-1]中子序列更大的一方作为[i,j]的结果。

5、需要注意循环的方向，比如位置 [2,3] 依赖的周围三个红色箭头。 所以我们需要横坐标倒序，纵坐标正序的进行计算。

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        # s[i:j] 中的最长回文子序列的长度是 dp[i][j]
        length = len(s)
        dp = [[0 for _ in range(length)] for _ in range(length)]
        
        # i 和 j 位置相同的时候为 1
        for i in range(length):
            dp[i][i] = 1
        for i in range(length - 1, -1, -1):
            for j in range(i + 1, length):
                if s[i] == s[j]:
                    dp[i][j] = dp[i + 1][j - 1] + 2
                else:
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
        
        return dp[0][length - 1]

题目 5. 最长回文子串

题目部分

给你一个字符串 s，找到 s 中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例 1：

输入：s = “babad”
输出：”bab”
解释：”aba” 同样是符合题意的答案。

解法

dp[i][j] 表示字符串s的下标范围 [i,j] 内最长回文子串的长度，如果不是最长回文子串，则为 0

这个解法，其实是跟上一个题对应着来实现的，主要区别有三点：

1、如果 s[i] != s[j]，那么 dp[i][j] 为 0 ，因为就不是回文串了。

2、如果 s[i] == s[j]，更新的时候还要满足 j - i == 1 or dp[i + 1][j - 1] != 0 ，也就是要么是 相邻的元素，可以从 0 开始 。如果不是相邻的元素，就不能从 0 开始了。 非回文串两侧即使增加了相同的元素，也不是回文串。

3、更新后的 max_length 需及时记录。

class Solution:
    def longestPalindrome(self, s: str) -> str:
        # 边界条件
        if len(s) == 0:
            return ""
        
        # s[i:j] 为最长回文子串的长度是 dp[i][j]
        length = len(s)
        dp = [[0 for _ in range(length)] for _ in range(length)]
        for i in range(length):
            dp[i][i] = 1
        
        max_length = 1
        max_str = s[0]
        
        for i in range(length - 1, -1, -1):
            for j in range(i + 1, length):
                if s[i] == s[j] and (j - i == 1 or dp[i + 1][j - 1] != 0):
                    dp[i][j] = dp[i + 1][j - 1] + 2
                
                if dp[i][j] > max_length:
                    max_length = dp[i][j]
                    max_str = s[i:j + 1]
        
        return max_str

小结

注意到，两个 dp 的定义其实是不一样的。 最长回文子序列中的 dp[0][length-1] 保留了最终的结果，而最长子串中 dp[i][j]仅为当前范围内的关系，最后收尾的位置不是最终结果。

造成这样区别的原因在于对转移条件方程中，是否有 else 的处理，子串是没有 else 处理的，而子序列是有的。

最长递增系列

最长递增系列题目难度要比回文系列简单不少，此类问题不需要考虑左边界的情况。（回文串是需要考虑左边界的）

题目 300. 最长递增子序列

题目部分

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。

例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

解法

我们不对 else 进行处理，因此 dp[i] 表示以 i 结尾的最长子序列的长度。

在本题中，dp[i] 可以表示以 i 结尾的、最长子序列长度。对于每一个位置 i，如果其之前的某个位置 j 所对应的数字小于位置 i 所对应的数字，则我们可以获得一个以 i 结尾的、长度为 dp[j] + 1 的子序列。为了遍历所有情况，我们需要 i 和 j 进行两层循环，其时间复杂度为 $O(n^2)$。

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        # dp[i] 截止到 i 位置最长递增子序列长度是多少
        n = len(nums)
        dp = [1] * n
        
        for i in range(n):
            # 对于每一个位置 i，如果其之前的某个位置 j 所对应的数字小于位置 i 所对应的数字
            for j in range(i):
                if nums[j] < nums[i]:
                    dp[i] = max(dp[i], dp[j] + 1)
        
        return max(dp)

题目 674. 最长连续递增序列

题目部分

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。

输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。

解法

class Solution:
    def findLengthOfLCIS(self, nums: List[int]) -> int:
        max_length = 1
        
        temp_length = 1
        for index, num in enumerate(nums):
            if index == 0:
                continue
            if num > nums[index - 1]:
                temp_length += 1
            else:
                temp_length = 1
            
            max_length = max(max_length, temp_length)
        return max_length

最长公共系列

题目 1143. 最长公共子序列

题目部分

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，”ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

输入：text1 = “abcde”, text2 = “ace”
输出：3
解释：最长公共子序列是 “ace” ，它的长度为 3 。

解法

定义 text1[:i-1] 与 text2[:j-1] 的最长公共子序列的长度是 dp[i][j]

class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        # 因为依赖于上一个位置， 所以 dp 长宽 + 1
        # 定义 text1[:i-1] 与 text2[:j-1] 的最长公共子序列的长度是 dp[i][j]
        m, n = len(text1), len(text2)
        dp = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
        
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if text1[i - 1] == text2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                else:
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
        return dp[m][n]

题目 最长公共子串

写法跟最长公共子序列基本是一样的，除了没有了那个 else，因此dp最后位置不是结果，需要手动计算。

题目 72. 编辑距离

题目部分

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

输入：word1 = “horse”, word2 = “ros”
输出：3
解释：
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)

解法

我们使用一个二维数组 dp[i][j]，表示将第一个字符串到位置 i 为止，和第二个字符串到位置 j 为止，最多需要几步编辑。

当第 i 位和第 j 位对应的字符相同时，dp[i][j]等于dp[i-1][j-1]；

当二者对应的字符不同时，有三种操作：

• 修改的消耗是dp[i-1][j-1]+1
• 插入 i 位置/删除 j 位置的消耗是dp[i][j-1] + 1
• 插入 j 位置/删除 i 位置的消耗是dp[i-1][j] + 1

class Solution:
    def minDistance(self, word1: str, word2: str) -> int:
        m = len(word1)
        n = len(word2)
        
        dp = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
        for i in range(m + 1):
            for j in range(n + 1):
                if i == 0:
                    # i 为 0 ，那就需要修改 j 步
                    dp[i][j] = j
                elif j == 0:
                    dp[i][j] = i
                elif word1[i - 1] == word2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1]
                elif word1[i - 1] != word2[j - 1]:
                    dp[i][j] = min(
                            dp[i - 1][j - 1] + 1,
                            dp[i - 1][j] + 1,
                            dp[i][j - 1] + 1)
        
        return dp[m][n]

小结

Q1: dp 什么时候长度为 n+1 ，什么时候是 n?

A1:

• 如果是单条内部进行对比，一般使用 dp[n]。如果是两条之前对比，一般使用 dp[m+1][n+1]。
• 是否需要 i - 1 位置上的元素，如果需要的话，那我们最好 n + 1，这样后续逻辑比较好处理。
• 是否需要取 dp[i] 的结果也是一个考量的指标，如果 dp[i]定义是第 i 个位置满足xxx条件，那么dp的长度就需要有 n+1，否则没法取 dp[n]