发表更新内容模态 / 自然语言处理40 分钟读完 (大约5985个字)

Transformer 中的 position embedding 的设计

前言

Transformer 使用 Attention 结构来进行建模，在 NLP 和 CV 领域都有比较好的效果，其主要结构如下：

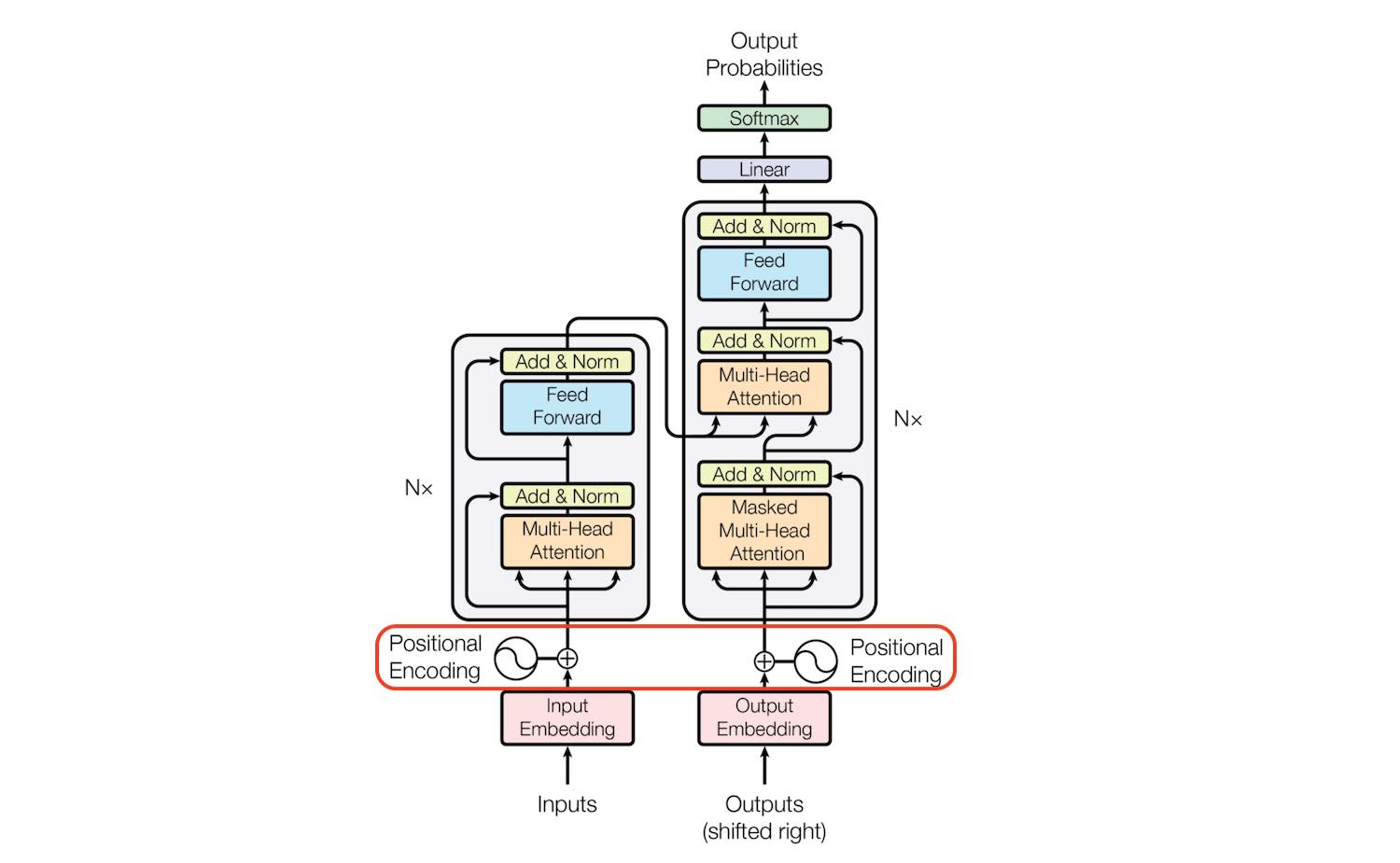
Transformer architecure

如果只取左边的部分，则退化为 BERT 类结构。 如果只取右边部分，则变成 GPT 类结构。

与lstm、rnn这种天然的流式结构不同，为了更高效地处理序列信息（并行计算），transformer的attention结构丢失了词汇的位置信息。如果不增加对位置信息的编码，则对于模型来说，乱序的词汇和正序的词汇没有分别。也即「今天 天气 真 好」和 「天气 真 今天 好」没有区别。

有两种常见的做法来引入位置关系：

  • 绝对位置编码：设法将位置信息合并到输入 embedding 中，以相加为主。
  • 相对位置编码：微调一下Attention结构，使得它有能力分辨不同位置的Token。

绝对位置编码

铺垫方法

用整型值标记位置

一种自然而然的想法是，给第一个token标记1，给第二个token标记2…，以此类推。这种方法产生了以下几个主要问题：

  • 模型可能遇见比训练时所用的序列更长的序列。不利于模型的泛化，外推性可能存在问题。
  • 模型的位置表示是无界的。随着序列长度的增加，位置值会越来越大。

用 [0,1] 范围标记位置

为了解决整型值带来的问题，可以考虑将位置值的范围限制在[0, 1]之内，其中，0表示第一个token，1表示最后一个token。比如有3个token，那么位置信息就表示成[0, 0.5, 1]；若有四个token，位置信息就表示成[0, 0.33, 0.69, 1]。 （这里有点像线性插值）。

当序列长度不同时，token间的相对距离是不一样的。例如在序列长度为3时，token间的相对距离为0.5；在序列长度为4时，token间的相对距离就变为0.33。

用二进制向量标记位置

考虑到位置信息作用在input embedding上，因此比起用单一的值，更好的方案是用一个和input embedding维度一样的向量来表示位置。这时我们就很容易想到二进制编码。如下图，假设d_model = 4，那么我们的位置向量可以表示成：

这里的变化是比较连续的，相近位置上的 embedding 距离也比较近。 但这种编码方式得到的位置编码处于一个离散空间中，我们很容易把 d_model = 4 个槽位用完，并且位置之间的距离变动可能会比较突兀。

如果能把离线空间转化为连续空间，就可以解决上述问题。

Sinusoidal

设计

其中 分别是位置 的编码向量的第 个分量， ​​ 是位置向量的维度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import torch
import math

def positional_encoding(seq_len, d_model):
    """ 
    seq_len: 输入序列的长度
    d_model: 模型的隐藏层维度
    """
    pos = torch.arange(seq_len, dtype=torch.float).unsqueeze(1)
    positional_embedding = torch.zeros((1, seq_len, d_model))
    
    div_term = torch.pow(10000.0, 2*torch.arange(0, d_model//2)/d_model) 

    positional_embedding[0, :, 0::2] = torch.sin(pos / div_term)
    positional_embedding[0, :, 1::2] = torch.cos(pos / div_term)
	
    """ 或者
    div_term = torch.exp(torch.arange(0, d_model, 2).float() * -(math.log(10000.0) / d_model))

    positional_embedding[0, :, 0::2] = torch.sin(pos * div_term)
    positional_embedding[0, :, 1::2] = torch.cos(pos * div_term)
    """
    return positional_embedding


# 展示为热力图
import seaborn as sns
import matplotlib.pyplot as plt

plt.figure(figsize=(18, 9))


%matplotlib inline
sns.set(font_scale=1.5)
sns.heatmap(data=pe.numpy()[0],cmap="RdBu_r")

可以看到 torch.pow(10000.0, 2*torch.arange(0, d_model//2)/d_model) 和公式内的方法并不一样，原始公式的实现更像是被注释掉的实现。

两者其实没有区别，但 ln10000 相较于 10000^x 相比，计算量要小一些，所以会做这种转化。

下图是一串序列长度为50，位置编码维度为128的位置编码可视化结果：

可以发现，由于sin/cos函数的性质，位置向量的每一个值都位于[-1, 1]之间。同时，纵向来看，图的右半边几乎都是红色的，这是因为越往后的位置， 越小，频率越小，波长越长，所以不同的t对最终的结果影响不大。而越往左边走，颜色交替的频率越频繁。

特性

如何理解Transformer论文中的positional encoding，和三角函数有什么关系？

https://kazemnejad.com/blog/transformer_architecture_positional_encoding/#proposed-method

https://blog.timodenk.com/linear-relationships-in-the-transformers-positional-encoding/

sinusoidal 编码的另外的一个重要能力，是通过绝对编码的方式实现了相对编码

We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset k, PEpos+k can be represented as a linear function of PEpos.

对于每组 sin-cos 都有对应的频率 ，为了方便公式定义，缩写其为 $\omega_k$。 需证明存在线性转化矩阵 (与 无关)满足如下等式：

证明：

令 为一个 的矩阵，我们定义 、、、 ，满足如下等式

三角函数

使用三角函数进行展开

于是得到了如下等式

通过解上述方程，得到了 、、、 的解

即 为：

可以看到，这里的矩阵 非常像旋转矩阵。

QA

  • postion embedding 为什么和 word embedding 相加？

这是一个历史非常悠久的问题，input_embedding = word_embedding + position_embedding + type_embedding ，3 种没有关系的 embedding 为什么可以直接相加呢。

有一些研究者给出了自己的答案，如 https://kazemnejad.com/blog/transformer_architecture_positional_encoding/#faq、[为什么 Bert 的三个 Embedding 可以进行相加？](https://www.zhihu.com/question/374835153) 。

我比较喜欢 保姆级教程，用PyTorch和BERT进行文本分类 - 机器学习社区的文章 - 知乎这个解释

Embedding 的数学本质，就是以 one hot 为输入的单层全连接。也就是说，世界上本没什么 Embedding，有的只是one hot。

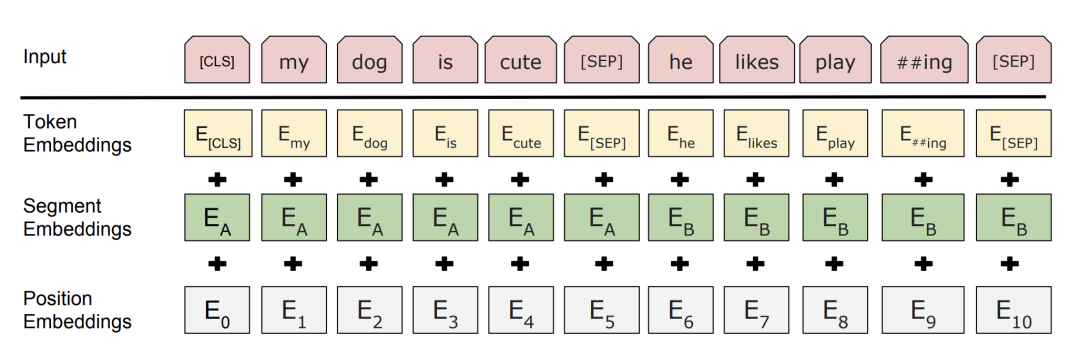
假设 token Embedding 矩阵维度是 [4,768]；position Embedding 矩阵维度是 [3,768]；segment Embedding 矩阵维度是 [2,768]。

对于一个字，假设它的 token one-hot 是[1,0,0,0]；它的 position one-hot 是[1,0,0]；它的 segment one-hot 是[1,0]。

那这个字最后的 word Embedding，就是上面三种 Embedding 的加和。

如此得到的 word Embedding，和concat后的特征：[1,0,0,0,1,0,0,1,0]，再过维度为 [4+3+2,768] = [9, 768] 的全连接层，得到的向量其实就是一样的。

  • BERT 内的 postion embedding 用的是 Sinusoidal 吗？

不是，说一千道一万，BERT 内的 position embedding 是直接学习出来的。这可能是因为 BERT 本身限制了512 长度，所以直接学习要比各种公式的尝试更快一些。 Sinusoidal 是 transformer 提出的，而 BERT 虽然基本采用了 encode 侧，但 position embedding 上有一些 diff。

相对位置编码

https://kexue.fm/archives/8130

相对位置并没有完整建模每个输入的位置信息，而是在算Attention的时候考虑当前位置与被Attention的位置的相对距离，由于自然语言一般更依赖于相对位置，所以相对位置编码通常也有着优秀的表现。

经典式

相对位置编码起源于Google的论文《Self-Attention with Relative Position Representations》，华为开源的NEZHA模型也用到了这种位置编码，后面各种相对位置编码变体基本也是依葫芦画瓢的简单修改。

一般认为，相对位置编码是由绝对位置编码启发而来，考虑一般的带绝对位置编码的Attention：

其中对那一维归一化，这里的向量都是指行向量。我们初步展开：

将 postion 相关的部分都丢弃掉，然后换上相对位置向量 ，得到了

以及换成：

所谓相对位置，是将本来依赖于二元坐标的向量，改为只依赖于相对距离$i-j$，并且通常来说会进行截断，以适应不同任意的距离

这样一来，只需要有限个位置编码，就可以表达出任意长度的相对位置（因为进行了截断），不管$\boldsymbol{p}_K,\boldsymbol{p}_V$是选择可训练式的还是三角函数式的，都可以达到处理任意长度文本的需求。

T5 类型

在之前的文章内提到过 T5 使用到的相对位置编码

img

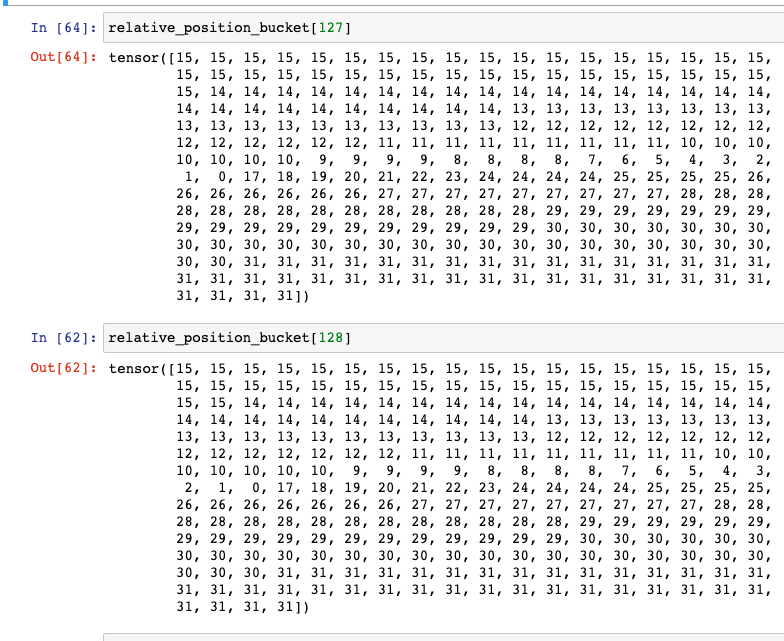
这个设计的思路其实也很直观，就是比较邻近的位置（0～7），我们需要比较得精细一些，所以给它们都分配一个独立的位置编码，至于稍远的位置（比如8～11），我们不用区分得太清楚，所以它们可以共用一个位置编码，距离越远，共用的范围就可以越大，直到达到指定范围再clip。

旋转位置编码

以下内容大幅引用自：https://zhuanlan.zhihu.com/p/670320068、https://zhuanlan.zhihu.com/p/642884818、https://kexue.fm/archives/9675、https://zhuanlan.zhihu.com/p/641274061、https://zhuanlan.zhihu.com/p/641865355、https://zhuanlan.zhihu.com/p/667864459

在这里先直接抛出一个直观的结论：RoPE位置编码通过将一个向量旋转某个角度，为其赋予位置信息。

RoPE的出发点

接下来进入今天的主角RoPE位置编码。在绝对位置编码中，尤其是在训练式位置编码中，模型只能感知到每个词向量所处的绝对位置，并无法感知两两词向量之间的相对位置。对于Sinusoidal位置编码而言，这一点得到了缓解，模型一定程度上能够感知相对位置。

对于RoPE而言，作者的出发点为：通过绝对位置编码的方式实现相对位置编码。回顾我们此前定义的位置编码函数，该函数表示对词向量 添加绝对位置信息 ，得到​ :

ROPE 希望 与 之间的点积， 即 中能够带有位置信息 。 那么 怎么才能算带有位置信息？ 只要能将 表示成一个关于 、、 的函数 即可，其中 便表示着两个向量之间的相对位置信息。

因此我们建模莫表就变成了，找到一个函数 ，使得如下关系成立：

二维位置编码

为了简化问题，我们先假设词向量是二维的。作者借助复数来进行求解，在此我们省略求解过程，直接抛出答案，最终作者得到如下位置编码函数，其中 为位置下标， 为一个常数：

为了更好地理解上面的函数，我们先简单复习一下线性代数中的旋转矩阵。在二维空间中，存在一个旋转矩阵 ，当一个二维向量左乘旋转矩阵时，该向量即可实现弧度为 的逆时针旋转操作。

我们以二维向量 为例，将其逆时针旋转45度，弧度为 ，将得到新的二维向量 ，向量的模长未发生改变，仍然是1。计算过程如下

回看我们求解得到的位置编码函数 ，我们得到的是一个向量旋转的函数，左侧的 是一个旋转矩阵， 表示在保持向量 的模长的同时，将其逆时针旋转 。这意味着只需要将向量旋转某个角度，即可实现对该向量添加绝对位置信息，这就是旋转位置编码的由来。

我们进一步验证RoPE是否能通过绝对位置编码的方式实现相对位置编码。当我们求两个向量之间的点积会发现，它们的点积是一个关于 、 、 的函数，所以函数 实现了以绝对位置编码的方式实现相对位置编码。

这里用到了三角函数的一些性质

为了更加形象生动地理解旋转位置编码，我们结合图形描述如何为一个二维向量赋予位置编码。假设存在向量 ，位置编码函数 中的 是一个常量，我们不妨设为1，则：

向量 位于位置0,1,2,3时，分别将向量 旋转0,1,2,3弧度，就可以为其赋予对应的绝对位置信息。如下图所示，只需要对向量进行旋转操作，即可对向量添加对应的位置信息。并且向量旋转具有周期性。

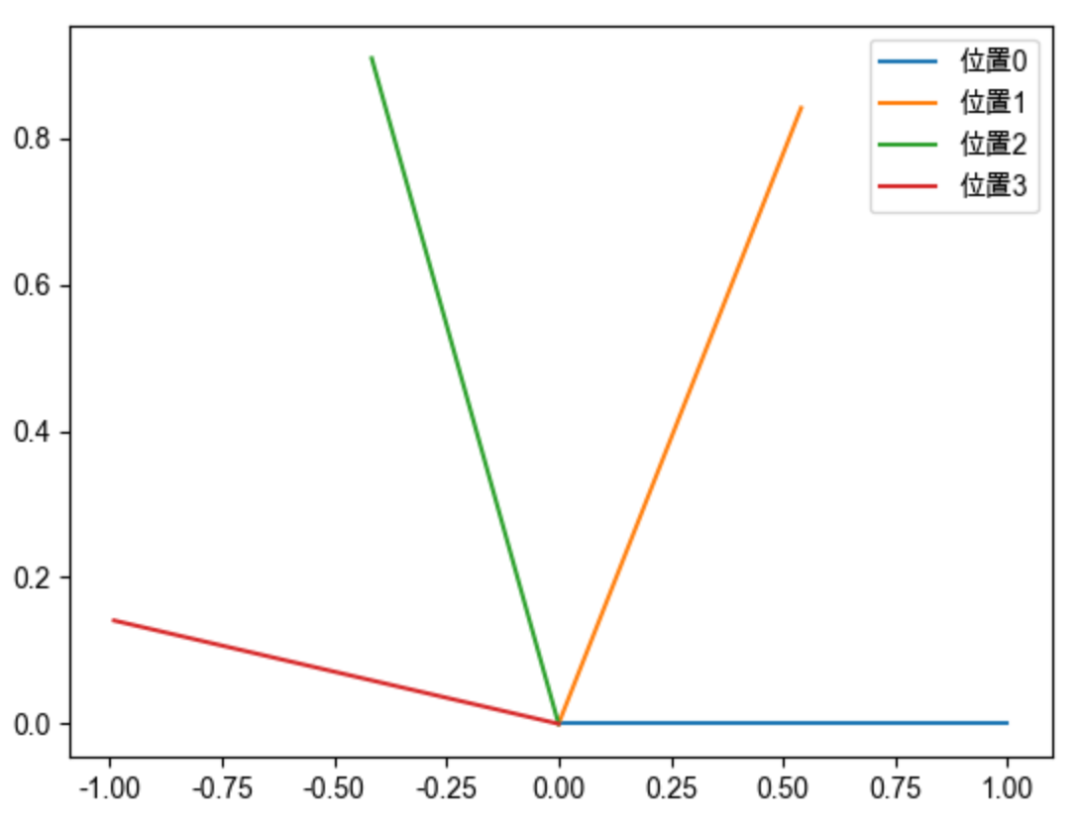
推广到多维

上述我们介绍了如何为一个二维向量赋予绝对位置信息：旋转一定的角度即可。但我们知道词向量的维度一般是几百甚至上千，如何将我们上述旋转的结论推广到多维呢？分而治之即可，我们把高维向量，两两一组，分别旋转。最终高维向量的旋转可表示成如下公式，可以认为左侧便是高维向量的旋转矩阵：

借鉴Sinusoidal位置编码，我们可以将每个分组的 设为不同的常量，从而引入远程衰减的性质。这里作者直接沿用了Sinusoidal位置编码的设置， 。则我们可以将高维向量的旋转矩阵更新为如下：

上式中的旋转矩阵十分稀疏，为了节省算力，可以以下面的方式等效实现：

我们继续随机初始化两个向量q和k，将q固定在位置0上，k的位置从0开始逐步变大，依次计算q和k之间的内积。我们发现随着q和k的相对距离的增加，它们之间的内积分数呈现出远程衰减的性质，这正是我们希望的。

代码实现

参考 https://nn.labml.ai/transformers/rope/index.html#section-1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class RotaryPositionalEmbeddings(nn.Module):
    
    def __init__(self, d: int, base: int = 10_000):
        
        super().__init__()

        self.base = base
        self.d = d
        self.cos_cached = None
        self.sin_cached = None

    def _build_cache(self, x: torch.Tensor):
        
        # 查看是否cache已存在
        if self.cos_cached is not None and x.shape[0] <= self.cos_cached.shape[0]:
            return

        # 序列长度
        seq_len = x.shape[0]

        # 按照上文所说的方式构造\theta_i
        theta = 1. / (self.base ** (torch.arange(0, self.d, 2).float() / self.d)).to(x.device)

        seq_idx = torch.arange(seq_len, device=x.device).float().to(x.device)

        # 不同位置的不同分量的\theta_i
        idx_theta = torch.einsum('n,d->nd', seq_idx, theta)

        idx_theta2 = torch.cat([idx_theta, idx_theta], dim=1) 
        # 更新cache
        self.cos_cached = idx_theta2.cos()[:, None, None, :]
        self.sin_cached = idx_theta2.sin()[:, None, None, :]

    def _neg_half(self, x: torch.Tensor):

        d_2 = self.d // 2

        return torch.cat([-x[:, :, :, d_2:], x[:, :, :, :d_2]], dim=-1)

    def forward(self, x: torch.Tensor):
        """
        x是query或者key的值，维度为 `[seq_len, batch_size, n_heads, d]`
        """
        # cache生成
        self._build_cache(x)

        # 选择一部分feature作用rope
        x_rope, x_pass = x[..., :self.d], x[..., self.d:]


        neg_half_x = self._neg_half(x_rope)

        x_rope = (x_rope * self.cos_cached[:x.shape[0]]) + (neg_half_x * self.sin_cached[:x.shape[0]])

        return torch.cat((x_rope, x_pass), dim=-1)

可以发现 x_rope = (x_rope * self.cos_cached[:x.shape[0]]) + (neg_half_x * self.sin_cached[:x.shape[0]]) 前边部分全是 cos、后半部分全是 sin， 。 相当于距离 的距离进行 pair。

旋转位置编码（Rotary Positional Encoding, RoPE）之所以称为“旋转”，是因为它通过旋转矩阵来编码位置信息。这种编码方式的核心思想是利用旋转来表示序列中元素的位置，从而在处理位置信息时保持一定的灵活性。

RoPE的关键优点包括：

  1. 可适应任意序列长度：它能够灵活地适应不同长度的输入序列。
  2. 随距离增加的依赖性衰减：随着序列中元素之间距离的增加，它们之间的依赖性逐渐减弱。
  3. 在线性自注意力中引入相对位置编码：RoPE能够为线性自注意力机制提供相对位置编码的能力。
  4. 通过绝对位置编码的方式，实现了相对位置编码：避免了 position embedding 与 word_embedding 相加的问题。

小结

  • 啥是外推性？

外推性是指大模型在训练时和预测时的输入长度不一致，导致模型的泛化能力下降的问题。例如，如果一个模型在训练时只使用了512个 token 的文本，那么在预测时如果输入超过512个 token，模型可能无法正确处理。这就限制了大模型在处理长文本或多轮对话等任务时的效果。

参考

Transformer 中的 position embedding 的设计

https://iii.run/archives/2b8191dac105.html

作者

mmmwhy

发布于

2024-02-06

更新于

2024-03-06

许可协议

#

评论

分类

×