范数计算

范数的计算主要使用到了 numpy.linalg.norm 函数，在数学推导中，范数是很常见的规则部分，但是具体的计算过程并不清楚，本篇尝试详细的计算一下。

Numpy函数

x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)

• x 表示矩阵
• ord 范数类型
• axis 计算的方向，比如横轴纵轴
• keepdims 是否保持原先的维度

范数的类型

ord	norm for matrices	norm for vectors
None	Frobenius norm	2-norm
‘fro’	Frobenius norm	–
‘nuc’	nuclear norm	–
inf	max(sum(abs(x), axis=1))	max(abs(x))
-inf	min(sum(abs(x), axis=1))	min(abs(x))
0	–	sum(x != 0)
1	max(sum(abs(x), axis=0))	as below
-1	min(sum(abs(x), axis=0))	as below
2	2-norm (largest sing. value)	as below
-2	smallest singular value	as below
other	–	$[\sum	x	^{ord}]^{1/ord}$

补充两点：

• $$||A||_F=[\sum_{i,j}abs(a_{i,j})^2]^{1/2}$$
• 核范数是奇异值的和

举例

根据Numpy给出的例子，进行分析：

import numpy as np
a = np.arange(9)-4
b = a.reshape(3,3)
print(a)
print(b)

得到：

a = [-4 -3 -2 -1  0  1  2  3  4]
b = [[-4 -3 -2]
    [-1  0  1]
    [ 2  3  4]]

向量范数

• 一范数: $||x||1 = \sum{i=1}^N|x_i|$ 即向量元素绝对值之和

  

• 二范数: $||\textbf{x}||2 =\sqrt{\sum{i=1}^Nx_i^2}$ uclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方

  

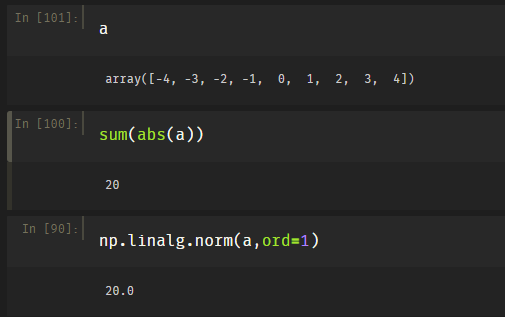
  可以看到np.linalg.norm(a)与np.linalg.norm(a, ord=2)的输出是一样的。

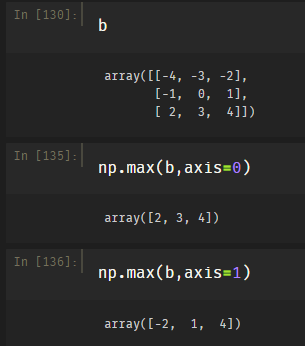
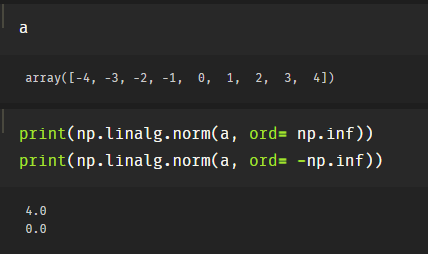
• $\infty$范数: $||\textbf{x}||_\infty = \max_{i}|x_i|$，即所有向量元素绝对值中的最大值

  $-\infty$范数: $||\textbf{x}||_{-\infty}=\min_i|x_i|$ ，即所有向量元素绝对值中的最小值

  

矩阵范数

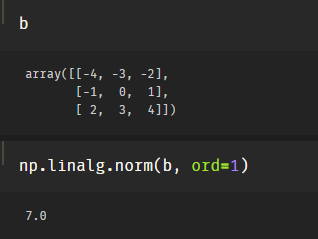
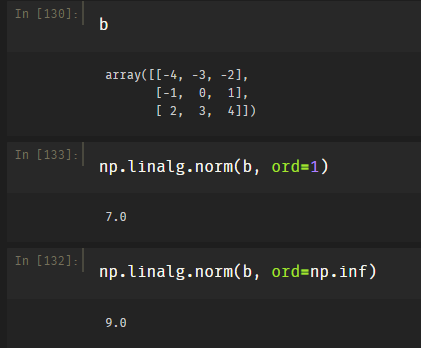
• 1-范数：$||A||_1 = \max_j\sum_{i=1}^m|a_{i,j}|$，列和范数，即所有矩阵列向量绝对值之和的最大值，可以理解为所有的数都是正数。

  

• 2-范数：$||A||_2 = \sqrt{\lambda_1}$ ，这里的$\lambda$是$A^TA$的最大特征值，也被称为谱范数，A’A矩阵的最大特征值的开平方。

  

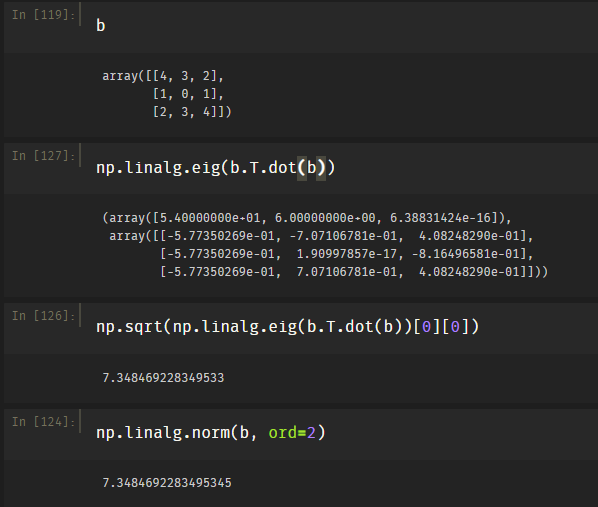
  np.linalg.eig 用于返回矩阵的特征值与特征向量。

• $\infty$-范数：$||A||_\infty = \max_i\sum_{j=1}^N|a_{i,j}|$，行和范数，即所有矩阵行向量绝对值之和的最大值。

  注意这个是行向量，而1-范数是列向量绝对值和。

  

范数计算

def normalizeRows(x):
    ### YOUR CODE HERE
    denom = np.apply_along_axis(lambda x: np.sqrt(x.T.dot(x)), 1, x)
    x /= denom[:, None]
    ### END YOUR CODE
    return x

或者 更简单

def normalizeRows(x):
    ### YOUR CODE HERE
    denom = np.linalg.norm(x,axis=1,keepdims=True)
    x = x/denom
    ### END YOUR CODE

    return x

Numpy中的Axis

设axis=i，则Numpy沿着第i个下标变化的方向进行操作。

举例：data =[[a00, a01],[a10,a11]]，

当axis = 0时，沿着第0个下标变化的方向进行操作，也就是a00->a10, a01->a11。

当axis = 1时，沿着第1个下标变化的方向进行操作，也就是a00->a01, a10->a11。