CS224n_Assignment_1
assignment1/index.html 第一次作业笔记,对应代码使用Jupyter实现参考链接。
Softmax
softmax常数不变性
由于$e^{x+y}=e^x * e^y$,因此多余的$e^c$可以上下消除,于是:
这里
发现了一个Softmax非常好的性质,即使两个数都很大比如 1000与 1001,其结果与 1和2的结果相同,即其只关注数字之间的差,而不是差占的比例。
实现
之所以介绍Softmax常数不变性,是因为发现给定的测试用例非常大,直接计算$e^x$次方会比较不可行。
神经网络基础
梯度检查
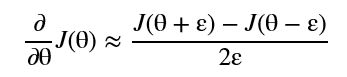
这里的random.setstate(rndstate)非常重要,因为后续会用到,主要部分为:
1 | x[ix] += h |
Sigmoid导数
定义$\sigma(x)$如下,发现$\sigma(x) + \sigma(-x) = 1$。
- sigmoid实现 $sigmoid(x)-=-\frac{1}{1+e^{(-x)} }$
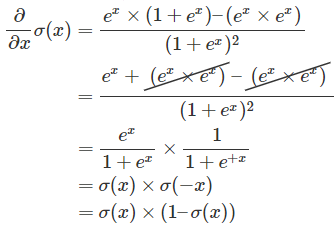
即: $\sigma’ = \sigma(x) \times (1-\sigma(x)) $
交叉熵定义
当使用交叉熵作为评价指标时,求梯度:
- 已知: $\hat{y} = softmax(\theta)$
- 交叉熵: $CE(y,\hat{y}) = - \sum_i{y_i \times log(\hat{y_i})}$
其中$\boldsymbol{y}$是指示变量,如果该类别和样本的类别相同就是1,否则就是0。因为y一般为one-hot类型。
而$\hat{y_i}$ 表示每种类型的概率,概率已经过softmax计算。
对于交叉熵其实有多重定义的方式,但含义相同:
分别为:
二分类定义
- y——表示样本的label,正类为1,负类为0
- p——表示样本预测为正的概率
多分类定义
- y——指示变量(0或1),如果该类别和样本的类别相同就是1,否则是0;
- p——对于观测样本属于类别c的预测概率。
但表示的意思都相同,交叉熵用于反映 分类正确时的概率情况。
Softmax导数
进入解答:
- 首先定义$S_i$和分子分母。
$S_i$对$\theta_j$求导:
注意: $S_i$分子是$\theta_i$ ,分母是所有的$\theta$ ,而求偏微的是$\theta_j$ 。
- 因此,根据i与j的关系,分为两种情况:
当 $ i == j$ 时:
当 $i \not= j $ 时:
交叉熵梯度
计算$\frac{\partial{CE} }{\partial{\theta_i} }$ ,根据链式法则,
因为,所以
反向传播计算神经网络梯度
根据题目给定的定义:
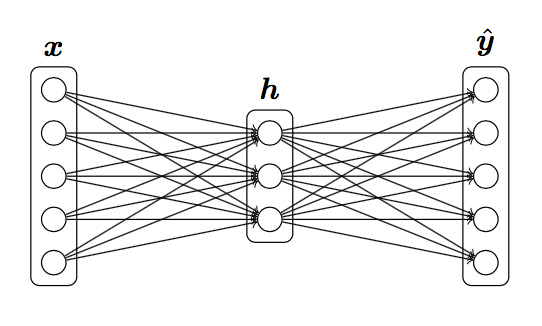
已知损失函数$J = CE$,$h = sigmoid(xW_1+b_1)$, $\hat{y} = softmax(hW_2+b_2)$
求$\frac{\partial{J} }{\partial{x} }$,$\frac{\partial{J} }{\partial{W_2} }$,$\frac{\partial{J} }{\partial{W1} }$,$\frac{\partial{J} }{\partial{b2} }$,$\frac{\partial{J} }{\partial{b_1} }$
解答:
反向传播,定义$z_2 = hW_2 + b_2$, $z_1 = xW_1 + b_1$:
对于输出层$\hat{y}$来说,$\hat{y}$的输入为 $z_2 = hW_2+b_2$,而输出则为 $\hat{y} = softmax(z_2)$
上小节计算得到 的梯度为 ,
可以使用 $z_2$ 替代 $\theta_i$ ,得到
$\delta_1 = \frac{\partial{CE} }{\partial{z_2} } = \hat{y} - y$
$\begin{align} \delta_2 = \frac{\partial{CE} }{\partial{h} } = \frac{\partial{CE} }{\partial{z_2} } \frac{\partial{z_2} }{\partial{h} } = \delta_1W_2^T \end{align}$
$\begin{align}\delta_3 = \frac{\partial{CE} }{z_1} = \frac{\partial{CE} }{\partial{h} }\frac{\partial{h} }{\partial{z_1} } = \delta_2 \frac{\partial{h} }{\partial{z_1} }= \delta_2 \circ \sigma’(z_1)\end{align}$ # 推测这里使用点乘的原因是$\delta_2 $经过计算后,应该是一个标量,而不是向量。
于是得到:$\frac{\partial{CE} }{\partial{x} }=\delta_3\frac{\partial{z_1} }{\partial{x} } = \delta_3W_1^T $
与计算$\frac{\partial{CE} }{\partial{x} }$相似,计算
- $\frac{\partial{CE} }{\partial{W_2} } = \frac{\partial{CE} }{\partial{z_2} }\frac{\partial{z_2} }{\partial{W_2} }=\delta_1 \cdot h$
- $\frac{\partial{CE} }{\partial{b_2} } = \frac{\partial{CE} }{\partial{z_2} }\frac{\partial{z_2} }{\partial{b_2} }=\delta_1$
- $\frac{\partial{CE} }{\partial{W_1} } = \frac{\partial{CE} }{\partial{z_1} }\frac{\partial{z_1} }{\partial{W_1} }=\delta_3 \cdot x$
- $\frac{\partial{CE} }{\partial{b_1} } = \frac{\partial{CE} }{\partial{z_1} }\frac{\partial{z_1} }{\partial{b_1} }=\delta_3$
参数数量
代码实现
如果仍然对反向传播有疑惑
- 可以参考一文弄懂神经网络中的反向传播法——BackPropagation,画图出来推导一下。
- 如何直观地解释 backpropagation 算法? - Anonymous的回答 - 知乎
https://www.zhihu.com/question/27239198/answer/89853077
word2vec
关于词向量的梯度
在以softmax为假设函数的word2vec中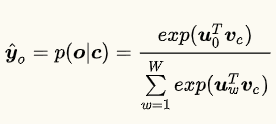
$\boldsymbol{v}_{c}$是中央单词的词向量
$\boldsymbol{u}_{w}$ ($w = 1,…,W$) 是第 $w$个词语的词向量。
假设使用交叉熵作为损失函数, $\boldsymbol{o}$ 为正确单词 (one-hot向量的第 $\boldsymbol{o}$维为1),请推导损失函数关于$\boldsymbol{v}_c$的梯度。
提示:
其中是所有词向量构成的矩阵。
解答:
首先明确本题给定的模型是skip-gram ,通过给定中心词,来发现周围词的。
定义$z=U^T \cdot v_c$ ,$U$ 表示所有词向量组成的矩阵,而$v_c$ 也表示的是一个词向量。
hint: 如果两个向量相似性越高,则乘积也就越大。想象一下余弦夹角,应该比较好明白。
因为$U$中所有的词向量,都和$v_c$乘一下获得$z$。
$z$是干嘛用的呢? $z$内就有W个值,每个值表示和$v_c$ 相似程度,通过这个相似度$softmax$选出最大值,然后与实际对比,进行交叉熵的计算。
已知: $\frac{\partial z}{\partial v_c} = U$ 和 $\frac{\partial J}{\partial \boldsymbol{z} } = (\hat{\boldsymbol{y} } -\boldsymbol{y})$
因此:$\frac{\partial J}{\partial{v_c} } =\frac{\partial J}{\partial \boldsymbol{z} } \frac{\partial z}{\partial v_c} = U(\hat{\boldsymbol{y} } -\boldsymbol{y})$
除了上述表示之外,还有另一种计算方法


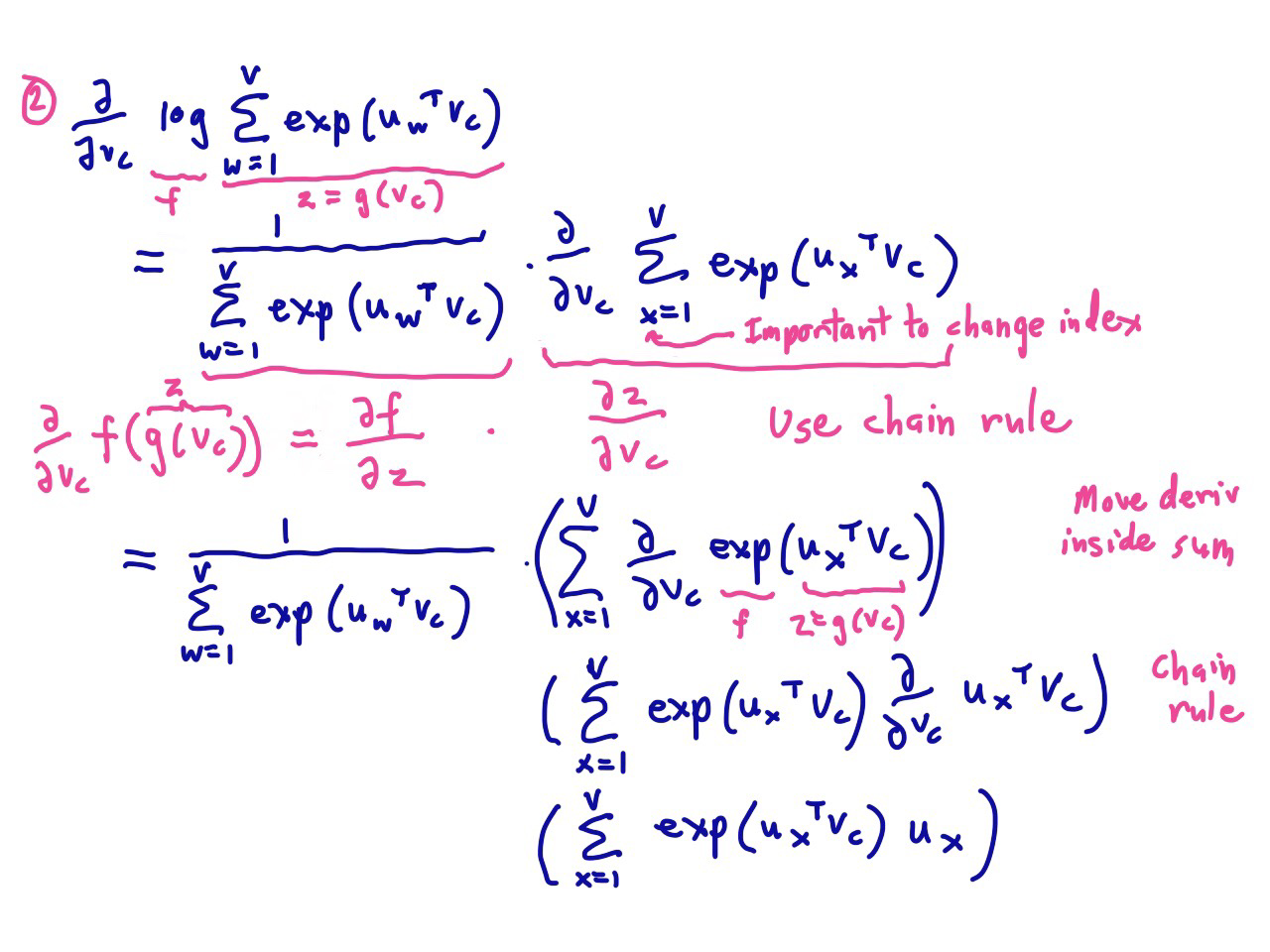

于是:
仔细观察这两种写法,会发现其实是一回事,都是 观察与期望的差($\hat{y} - y$)。
推导lookup-table梯度
与词向量相似
$\frac{\partial J}{\partial{U} } =\frac{\partial J}{\partial \boldsymbol{z} } \frac{\partial z}{\partial U} = v_c(\hat{\boldsymbol{y} } -\boldsymbol{y})^{T}$
代码实现
负采样时的梯度推导
假设进行负采样,样本数为$\boldsymbol{K}$,正确答案为$\boldsymbol{o}$,那么有$o \notin {1,…,K}$。负采样损失函数定义如下:
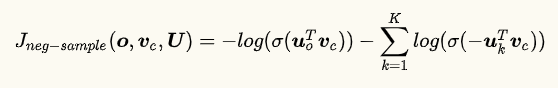
其中:
解答:
首先说明一下,$J_{neg-sample}$从哪里来的,参考note1 第11页,会有一个非常详细的解释。
代码实现
全部梯度
推导窗口半径$m$的上下文时,skip-gram 和 CBOW的损失函数 ( 是正确答案的词向量)或说 或 关于每个词向量的梯度。
对于skip-gram来讲,$c$的上下文对应的损失函数是:
这里 $\boldsymbol{w}_{c+j}$ 是离中心词距离$j$的那个单词。
而CBOW稍有不同,不使用中心词$\boldsymbol{v}_{c}$而使用上下文词向量的和$\hat{\boldsymbol{v} }$作为输入去预测中心词:
然后CBOW的损失函数是:
解答:
根据前面的推导,知道如何得到梯度
和
那么所求的梯度可以写作:
skip-gram
CBOW
代码实现
补充部分
矩阵的每个行向量的长度归一化
1
x = x/np.linalg.norm(x,axis=1,keepdims=True)
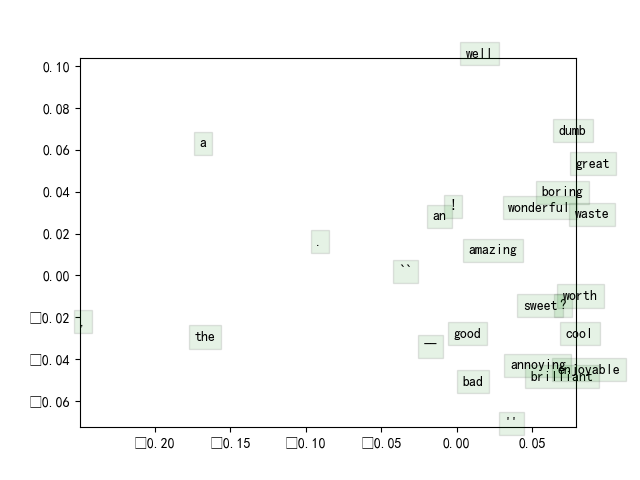
情感分析
特征向量
最简单的特征选择方法就是取所有词向量的平均
1 | sentence_index = [tokens[i] for i in sentence] |
正则化
1 | values = np.logspace(-4, 2, num=100, base=10) |
调参
1 | bestResult = max(results, key= lambda x: x['dev']) |
惩罚因子对效果的影响
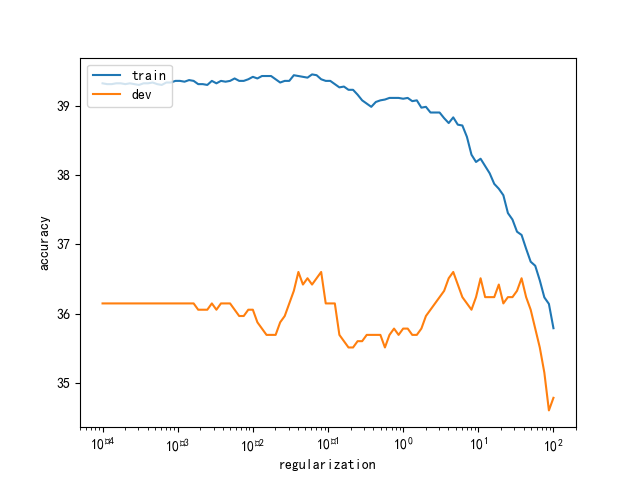
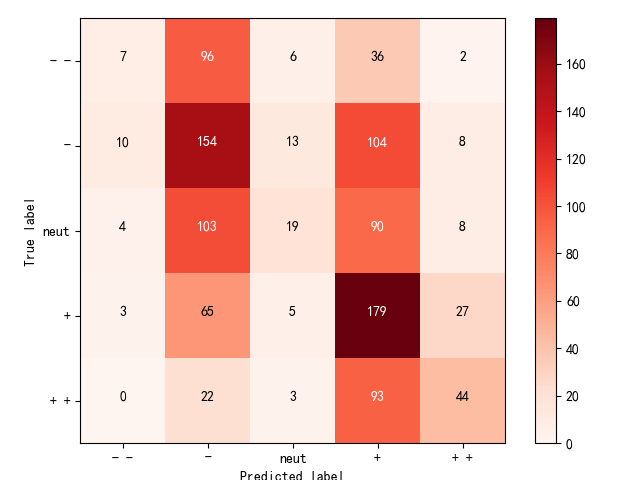
confusion matrix
关联性排序的一个东西,对角线上的元素越多,预测越准确。
代码参考
CS224n_Assignment_1