Coursera ML(6)-Neural Networks Representation
神经网络模型
Neural Networks Model
A single neuron model: logistic unit
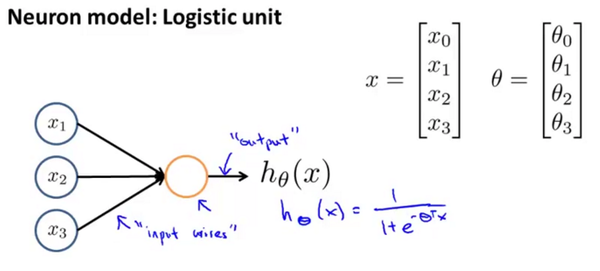
- Takes 3+1 inputs(the extra input called bias is just like $θ_0$ in logistic regression, not shown in picture).
- Both input and output could be represented as vectors, in which each unit has its own parameters $θ$
- All the units in the same layer take the same input $x$, as the pic shows.
- Each unit has only one output: $sigmoid(θ^Tx)$. Of course there’re other choices for sigmoid function.
Neural Networks
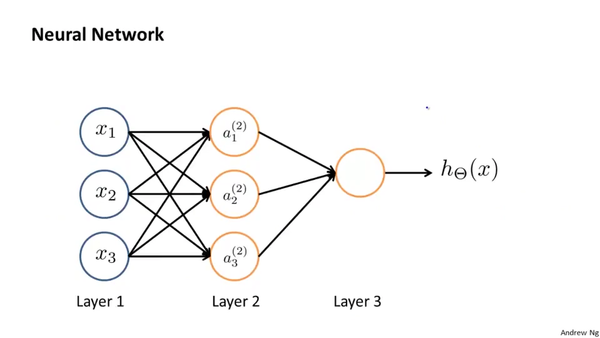
其中
Calculation from one layer to the next
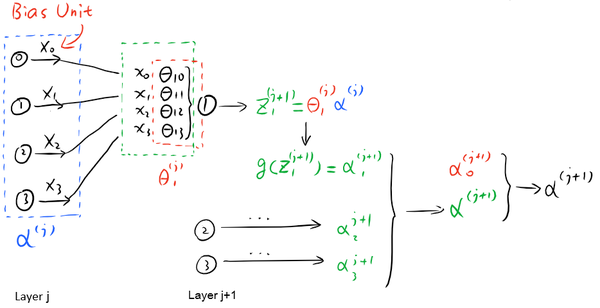
In the picture above, we have the networks from layer j to layer j+1, in which layer j has 3(+1) units while layer j+1 has 3 layers. Let $s_j=3$, $s_j+1=3$
- $α^{(j)}$ : Output of the $j_{th}$ layer. $s_j+1$ dimension vector.
- $θi^{(j)}$ : Parameters in the $i{th}$ unit of $(j+1)_{th}$ layer. $s_j+1$ dimension vector.
- ${\theta^{(j)} } = \begin{bmatrix} \theta1^{(j)} & \theta_2^{(j)} & \cdots & \theta{s(j + 1)}^{(j)} \end{bmatrix}^T$ : All the network parameters from $j{th}$ layer to ${(j+1)}_{th}$ layer.
- We have: $\alpha^{(j+1)} = sigmoid(\mathbf{\theta^{(j)} }\alpha^{(j)})$ add $\alpha_0^{(j+1)}$
Multiclass Classification
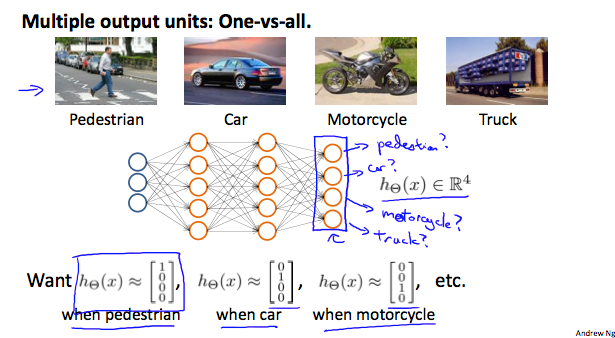
Each $y^{(i)}$ represents a different image corresponding to either a car, pedestrian, truck, or motorcycle. The inner layers, each provide us with some new information which leads to our final hypothesis function. The setup looks like:
Summary

Example: layer 1 has 2 input nodes and layer 2 has 4 activation nodes. Dimension of $\Theta^{(1)}$ is going to be 4×3 where $sj = 2$ and $s{j+1} = 4$, so $s_{j+1} \times (s_j + 1) = 4 \times 3$$
今天苏州的天气真是闷热,实在是看不下去了。因此本小节笔记,有大段参考自 shawnau.github.io
Coursera ML(6)-Neural Networks Representation