推荐指标-NDCG

NDCG，Normalized Discounted cumulative gain 直接翻译为归一化折损累计增益，这个指标通常是用来衡量和评价搜索结果算法。

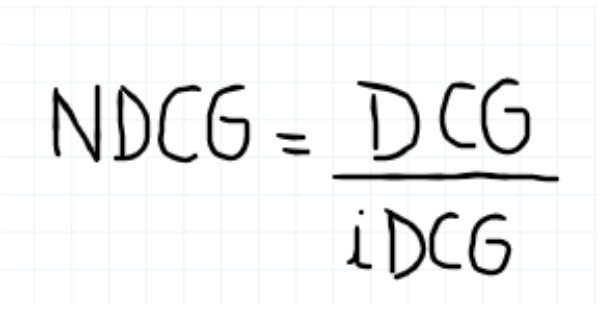
概念

DCG的两个思想：

　　1、高关联度的结果比一般关联度的结果更影响最终的指标得分；

　　2、有高关联度的结果出现在更靠前的位置的时候，指标会越高;

累计增益(CG)

CG，cumulative gain，是DCG的前身，只考虑到了相关性的关联程度，没有考虑到位置的因素。它是一个搜素结果相关性分数的总和。指定位置p上的CG为：

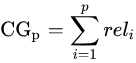
reli 代表i这个位置上的相关度。

举例：假设搜索“篮球”结果，最理想的结果是：B1、B2、 B3。而出现的结果是 B3、B1、B2的话，CG的值是没有变化的，因此需要下面的DCG。

折损信息增益(DCG)

DCG， Discounted 的CG，就是在每一个CG的结果上处以一个折损值，为什么要这么做呢？目的就是为了让排名越靠前的结果越能影响最后的结果。假设排序越往后，价值越低。到第i个位置的时候，它的价值是 1/log2(i+1)，那么第i个结果产生的效益就是 reli * 1/log2(i+1)，所以：

归一化折损累计增益（NDCG）

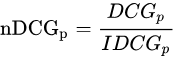
IDCG为理想情况下最大的DCG值。

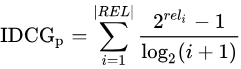
　　其中 |REL| 表示，结果按照相关性从大到小的顺序排序，取前p个结果组成的集合。也就是按照最优的方式对结果进行排序。

实际的例子

　　假设搜索回来的5个结果，其相关性分数分别是 3、2、3、0、1、2

　　那么 CG = 3+2+3+0+1+2

　　可以看到只是对相关的分数进行了一个关联的打分，并没有召回的所在位置对排序结果评分对影响。而我们看DCG：

所以 DCG = 3+1.26+1.5+0+0.38+0.71 = 6.86

　　接下来我们归一化，归一化需要先结算 IDCG，假如我们实际召回了8个物品，除了上面的6个，还有两个结果，假设第7个相关性为3，第8个相关性为0。那么在理想情况下的相关性分数排序应该是：3、3、3、2、2、1、0、0。计算IDCG@6:

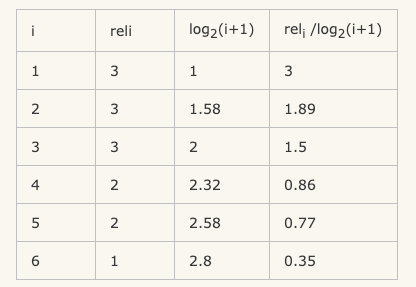
所以IDCG = 3+1.89+1.5+0.86+0.77+0.35 = 8.37

　　so 最终 NDCG@6 = 6.86/8.37 = 81.96%

实现代码

def get_dcg(y_pred, y_true,k):
    #注意y_pred与y_true必须是一一对应的，并且y_pred越大越接近label=1(用相关性的说法就是，与label=1越相关)
    df = pd.DataFrame({"y_pred":y_pred, "y_true":y_true})
    df = df.sort_values(by="y_pred", ascending=False)  # 对y_pred进行降序排列，越排在前面的，越接近label=1
    df = df.iloc[0:k, :]  # 取前K个
    dcg = df["y_true"] / np.log2(np.arange(1, df["y_true"].count()+1) + 1) # 位置从1开始计数
    dcg = np.sum(dcg)
    return dcg

def get_ndcg(y_pred, y_true,k=5):
    # df包含y_pred和y_true
    dcg = get_dcg(y_pred, y_true,k)
    idcg = get_dcg(y_true, y_true,k)
    ndcg = dcg / idcg
    return ndcg

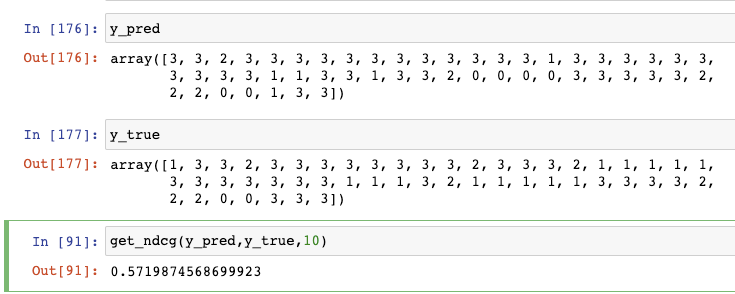
即为 ndcg@10了

参考 https://www.cnblogs.com/by-dream/p/9403984.html