Coursera ML(4)-Logistic Regression
本节笔记对应第三周Coursera课程 binary classification problem
Classification is not actually a linear function.
Classification and Representation
Hypothesis Representation
- Sigmoid Function(or we called Logistic Function)Sigmoid Function 可以使输出值范围在$(0,1)$之间。$g(z)$对应的图为:
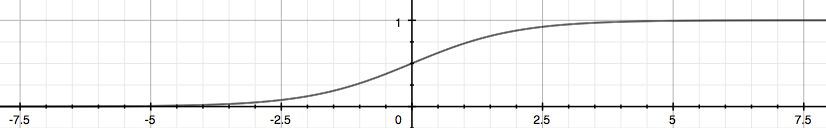
- $h_\theta(x)$ will give us the probability that our output is 1.
- Some basic knowledge of discrete
Decision Boundary
- translate the output of the hypothesis function as follows:
- From these statements we can now say:
Logistic Regression Model
Cost function for one variable hypothesis
- To let the cost function be convex for gradient descent, it should be like this:
- example
Simplified Cost Function and Gradient Descent
compress our cost function’s two conditional cases into one case:
entire cost function
Gradient Descent
the general form of gradient descent ,求偏导的得到$J(\theta)$的极值
using calculus
get
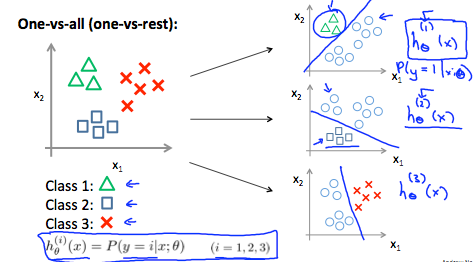
Multiclass Classification: One-vs-all
- For more than 2 features of y, do logisitc regression for each feature separately
- Train a logistic regression classifier $h_\theta(x)$ for each class to predict the probability that  y = i .
- To make a prediction on a new x, pick the class that maximizes $ h_\theta (x) $
Solving the Problem of Overfitting
The Problem of Overfitting
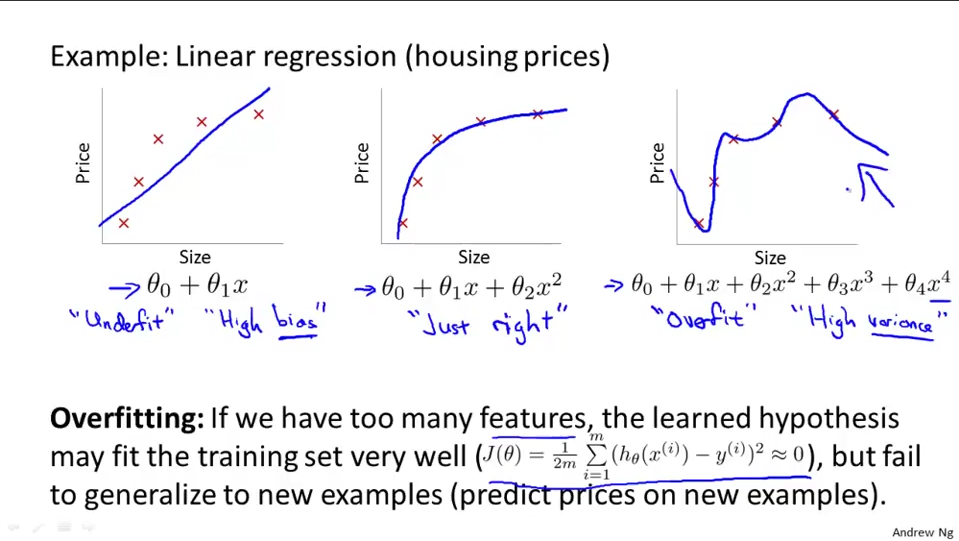
address the issue of overfitting
- Reduce the number of features:
- Manually select which features to keep.
- Use a model selection algorithm (studied later in the course).
- Regularization:
- Keep all the features, but reduce the magnitude of parameters $θ_j$.
- Regularization works well when we have a lot of slightly useful features.
Cost Function
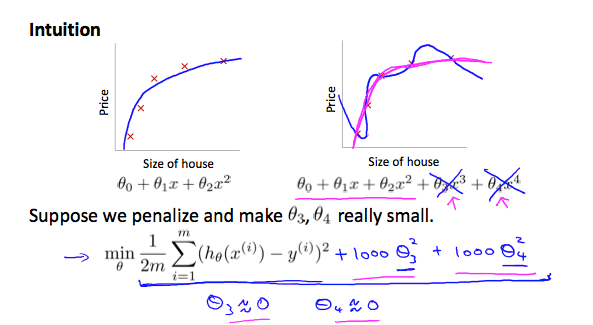
- in a single summation
The λ, or lambda, is the regularization parameter. It determines how much the costs of our theta parameters are inflated.
Regularized Linear Regression
Gradient Descent
Normal Equation
- L is a matrix with 0 at the top left and 1’s down the diagonal, with 0’s everywhere else. It should have dimension (n+1)×(n+1)
- Recall that if m ≤ n, then $X^TX$ is non-invertible. However, when we add the term λ⋅L, then $X^TX + λ⋅L $becomes invertible.
Summary
我在这里整理一下上述两个方法,补全课程上的相关推导。
Logistic Regression Model
$h_\theta(x)$是假设函数
注意假设函数和真实数据之间的区别
Cost Function
回头看看上边的那个$h_\theta (x)$ ,cost function定义了训练集给出的结果 和 当前计算结果之间的差距。当然,该差距越小越好,那么需要求导一下。
Gradient Descent
- 原始公式
- 求导计算
- 计算结果
这里推导一下$\frac{\partial}{\partial \theta_j} J(\theta)$:
计算$h_\theta’(x)$导数
推导$\frac{\partial}{\partial \theta_j} J(\theta)$
即:
Solving the Problem of Overfitting
其他地方都一样,稍作修改
Cost Function
Gradient Descent
以上
Coursera ML(4)-Logistic Regression