发表更新代码能力 / 总结16 分钟读完 (大约2362个字)

算法实验(一)

快速排序与背包问题相关算法分析

快速排序

相关文章

普通快速排序

算法效率：

  • 最坏情况下分析：当输入序列是正序或者是反序的时候，效率最坏，这时效率是$Θ(n^2)$
  • 最优情况下分析：其他情况下的算法效率趋向于$Θ（nlgn）$

    伪代码

    对整个数组进行递归排序：
    1
    2
    3
    4
    5
    QUICKSORT(A,p,r)
    if p < r:
        q = PARTITION(A,p,r);
        QUICKSORT(A,p,q-1);
        QUICKSORT(A,q+1,r);
    快速排序算法的关键是PARTITION过程，它对A[p..r]进行就地重排：
    1
    2
    3
    4
    5
    6
    7
    8
    9
    PARTITION(A,p,r)
    x = A[r]
    i = p-1
    for j = p to r-1// A[j]是待比较的元素
      if A[j] ≤ r// 若A[j]比主元小
        i = i + 1 // i往后一位（符合，不用替换；不符合i就停在这个地方，等着j过来叫唤）
        exchange A[i] with A[j]//倘若A[j]比主元小，其实是不发生交换的。
    exchange A[i+1] with A[r]
    return i + 1

    python代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    # coding=utf-8
    import datetime
    import sys   
    sys.setrecursionlimit(1000000)
    def SET_NUMBER():
        l = []
        for i in range(0,len(range(1,2000,2)[::-1])-1):
            l.append(range(1,2000,2)[::-1][i])
        return l
            
    def PARTITION(A,p,r):
        x = A[r]
        i = p - 1
        for j in range(p,r):
            if A[j]<=x:
                i = i + 1
                A[i],A[j]=A[j],A[i]
        A[i+1],A[r] = A[r],A[i+1]
        return i+1


    def QUICKSORT(A,p,r):
        if p >= r:
            return
        q = PARTITION(A,p,r)
        QUICKSORT(A,p,q-1)
        QUICKSORT(A,q+1,r)
        
    if __name__ == '__main__':
        l = SET_NUMBER()
        time1 = datetime.datetime.now()
        QUICKSORT(l,0,len(l)-1)
        time2 = datetime.datetime.now()
        print(time2-time1)

随机快速排序

算法效率

我们已经知道，若输入本身已被排序，那么对于快排来说就糟了。那么如何避免这样的情况？一种方法时随机排列序列中的元素；另一种方法时随机地选择主元（pivot）。这便是随机化快速排序的思想，这种快排的好处是：其运行时间不依赖于输入序列的顺序。

经分析， 随机化快排的算法效率是$Θ(nlgn)$

伪代码

下面是分化（Partition）

1
2
3
4
Random_Partition(vector<T> &A,int p,int q)
    int i=rand()%(q-p)+p;  //此行与快排不同、加入随机数参数器
    Swap(A[i],A[p]);         //此行与快排不同、随机选取主元
    return Partition(A,p,q);//此次与快速排序一样

随机化快速排序
1
2
3
4
5
Random_Quick_Sort(vector<T> &A,int p,int q)
    if (p<q):
        int i=Random_Partition(A,p,q);
        Random_Quick_Sort(A,p,i-1);
        Random_Quick_Sort(A,i+1,q);

python代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# coding=utf-8
import datetime
import random
def SET_NUMBER():
    l = []
    for i in range(0,len(range(1,2000,2)[::-1])-1):
        l.append(range(1,2000,2)[::-1][i])
    return l


def PARTITION(A,p,r):
    x = A[r]
    i = p - 1
    for j in range(p,r):
        if A[j]<=x:
            i = i + 1
            A[i],A[j]=A[j],A[i]
    A[i+1],A[r] = A[r],A[i+1]
    return i+1

def Random_Partition(A,p,r):
    i = random.randint(p, r) 
    A[i],A[p]=A[p],A[i]
    return PARTITION(A,p,r)

def QUICKSORT(A,p,r):
    if p >= r:
        return
    q = Random_Partition(A,p,r)
    QUICKSORT(A,p,q-1)
    QUICKSORT(A,q+1,r)
    
if __name__ == '__main__':
    l = SET_NUMBER()
    time1 = datetime.datetime.now()
    QUICKSORT(l,0,len(l)-1)
    time2 = datetime.datetime.now()
    print(time2-time1)

时间效率

  • 对于倒序数组range(1,2000,2)[::-1](1000个数字)
    • 使用正常快速排序时间为：0:00:00.082566
    • 使用随机快速排序时间为：0:00:00.005815
  • 对于随机数组random.randint(0,9999)(重复1000次)
    • 使用正常快速排序时间为：0:00:00.002974
    • 使用随机快速排序时间为：0:00:00.004901

分析性能差异

快速排序的平均时间复杂度为$O(nlogn)$，最坏时间时间可达到$O(n^2)$，最坏情况是当要排序的数列基本有序的时候。根据快速排序的工作原理我们知道，选取第一个或者最后一个元素作为主元，快速排序依次将数列分成两个数列，然后递归将分开的数列进行排序。

当把数列平均分成两个等长的数列时，效率是最高的，如果相差太大，效率就会降低。

我们通过使用随机化的快速排序随机的从数列中选取一个元素与第一个，或者最后一个元素交换，这样就会使得数列有序的概率降低。

所以随机快速排序平均速度是比快速排序要快的，但是因为随机排序需要有设置随机数+交换元素的时间，因此总时间上不如普通快速排序。

背包问题

相关文章

动态规划知识复习

基本步骤

  • 找出最优解的性质，并刻画其结构特征
  • 递归地定义最优解的值
  • 以自底而上的方式计算出最优值
  • 根据计算最优值时得到的信息，构造一个最优解。

    若给定问题具有以下性质：

  • 最优子结构：如果一个问题的最优解中包含了其子问题的最优解，就说该问题具有最优子结构。当一个问题具有最优子结构时，提示我们动态规划法可能会适用，但是此时贪心策略可能也是适用的。
  • 重叠子问题：指用来解原问题的递归算法可反复地解同样的子问题，而不是总在产生新的子问题。即当一个递归算法不断地调用同一个问题时，就说该问题包含重叠子问题。此时若用分治法递归求解，则每次遇到子问题都会视为新问题，会极大地降低算法的效率，而动态规划法总是充分利用重叠子问题，对于每个子问题仅计算一次，把解保存在一个在需要时就可以查看的表中，而每次查表的时间为常数。

0-1背包问题

定义问题

问题：有n个物品，第i个物品价值为$v_i$，重量为$w_i$，其中$v_i$和$w_i$均为非负数，背包的容量为W，W为非负数。现需要考虑如何选择装入背包的物品，使装入背包的物品总价值最大。

该问题以形式化描述如下：

  • 目标函数为 ：
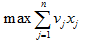
    1554979485.png
  • 约束条件为：
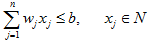
    1554979494.png
    满足约束条件的任一集合（x1，x2，…，xn）是问题的一个可行解，问题的目标是要求问题的一个最优解。考虑一个实例，假设n=5，W=17， 每个物品的价值和重量如下表所示。可将物品1，2和5装入背包，背包未满，获得价值22，此时问题解为你（1，1，0，0，1）。也可以将物品4和5装入背包，背包装满，获得价值24，此时解为（0，0，0，1，1）。
    1554979562.png

按步骤求解问题

  • 找出最优解的性质，并刻画其结构特征
    可以将背包问题的求解过程看作是进行一系列的决策过程，即决定哪些物品应该放入背包，哪些物品不放入背包。如果一个问题的最优解包含了物品n，即$xn=1$，那么其余$x_1，x_2，…，x(n-1)$一定构成子问题1，2，…，n-1在容量W-wn时的最优解。如果这个最优解不包含物品n，即$xn$=0，那么其余$x_1，x_2，…，x(n-1)$一定构成子问题1，2，…，n-1在容量W时的最优解。
  • 递归定义最优解的值
    根据上述分析的最优解的结构递归地定义问题最优解。设c[i,w]表示背包剩余容量为w时，i个物品导致的最优解的总价值。
    分为三种情况：
    • i或者w等于0，没有空间也没有物品的时候；
    • 第i的物品的重量已经超过当前空间时；
    • 在增加第i个物品和不增加第i个物品之间做出艰难的抉择；
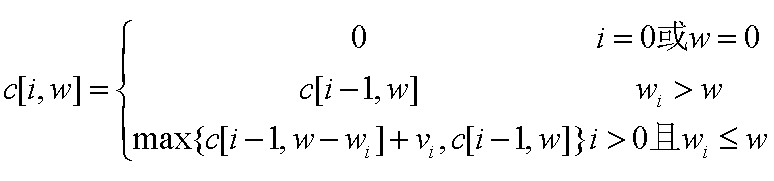
      1554979734.png
  • 以自底而上的方式计算出最优值
    伪代码：
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    BOTTOM-UP-CUT-ROD(p,n)
    let  r[0..n] be a new array
    r[0]= 0
    for  j = 1 to n
        q= -∞
        for  i = 1 to j
            q = max(q, p[i]+r[j-i])
        r[j]= q
    return  r[n]

python代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#coding:utf-8  
def bag(n,m,w,v):  
    res = [[0 for j in range(m+1)]for i in range(n+1)] #n+1 行，m+1列 值为0的矩阵  
    for i in range(1,n+1):  
        for j in range(1,m+1):  
            res[i][j] = res[i-1][j] #0->res[0][1]->res[1][1]  
            if j>=w[i-1] and res[i][j]<res[i-1][j-w[i-1]]+v[i-1]:#如果res[i-1][j]小于res[i-1][j-w[i-1]]+v[i-1]，那么res[i][j]就等于res[i-1][j]，否则就等于res[i-1][j-w[i-1]]+v[i-1]  
                res[i][j] = res[i-1][j-w[i-1]]+v[i-1]  
    return res  
  
def show(n,m,w,res):  
    print (u"最大值为%d"%res[n][m]) 
    x = [False for i in range(n)]  
    j = m  
    for  i in range(n,0,-1):  
        if res[i][j]!=res[i-1][j]:  
            x[i-1] = True  
            j-=w[i-1]  
    print (u"选择的物品为")  
    for i in range(n):  
        if x[i]:  
            print(u"第%d个"%(i+1))  
  
if __name__ == "__main__":  
    #n种物品，承重量为m，w物品的重量，v 物品的价值  
    n= 5  
    m = 17  
    w = [3,4,7,8,9] 
    v = [4,5,10,11,13]  
    res = bag(n,m,w,v)  
    show(n,m,w,res)

部分背包问题

题目要求使用贪心算法

  • 部分背包问题与0-1背包问题的差别在于：可以带走一部分。即，部分背包问题可带走的物品 是可以 无限细分的。
  • 贪心策略是：总是优先选择单位重量下价值最大的物品

    具体题目

    假设背包可容纳50Kg的重量，物品信息如下：
物品 i 重量(Kg) 价值 单位重量的价值
1 10 60 6
2 20 100 5
3 30 120 4

伪代码

这个看起来就很简单，先装单价最高的1，剩下的地方装2，再剩下的地方装3
我也不知道怎么写伪代码，直接写python吧

C代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <stdio.h>  
#include <algorithm>  
using namespace std;  
  
  
//物品结构体，包含两个属性，w表示重量，v表示价值  
struct Good{  
    int id;  
    double w;  
    double v;  
};  
  
//排序比较函数，以物品的价值/重量比值降序排序  
bool cmp(Good a, Good b){  
    if (a.v/a.w > b.v/b.w) {  
        return true;  
    }  
    return false;  
}  
  
//结构体数组,所有物品信息  
struct Good goods[] = { {1,10,12},{2,9,9},{3,11,7},{4,12,9},{5,6,8},{6,3,4} };  
  
  
//背包总重量  
double totalW = 30;  
  
int main()  
{  
    //以物品的价值/重量比值降序排序  
    sort(goods,goods+6,cmp);  
    double leftW = totalW;  
    int totalV = 0;  
      
    //遍历排好序的物品数组  
    for (int i=0; i<6; i++) {  
        //如果当前背包所能承受的重量大于i物品的总量  
        //那么把i物品全部放进去  
        if (leftW >= goods[i].w) {  
            leftW -= goods[i].w;  
            totalV += goods[i].v;  
            printf("choose good[id = %d], %.1f weight,make %.1f value\n",goods[i].id,goods[i].w,goods[i].v);  
              
        //如果不能，那么取当前背包所能承受重量的相应数量物品  
        //当然价值也得按照比例来  
        }else {  
            totalV += leftW/goods[i].w * goods[i].v;  
            leftW = 0;  
            printf("choose good[id = %d], %.1f weight,make %.1f value\n",goods[i].id,leftW,leftW/goods[i].w * goods[i].v);  
            break;  
        }  
    }  
      
    printf("max total value:%d\n",totalV);  
    return 0;  
}

算法实验(一)

https://iii.run/archives/418837ed23d7.html

作者

mmmwhy

发布于

2017-05-24

更新于

2022-10-30

许可协议

#

评论

分类

×