NLP 之 n-gram

N-Gram 模型

N-Gram 模型基于这样一个假设，第 n 个词的出现只与前边的 n-1 个词有关，与其他的任何词都不相关，整句的概率就是各个词出现的概率的乘积。

这些概率可以通过直接从语料中统计n个词同时出现的次数得到，常用的是二元的Bi-Gram和三元的Tri-Gram。

原始问题

假设我们目前有一个句子T，句子T有许多个词组成。

现在我来考虑一下这个句子出现的概率也就是：

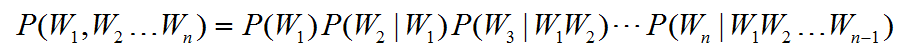
比方说，今天天气真好，这个句子出现的概率。就应该是：

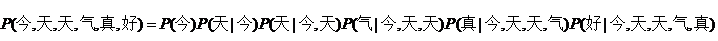
现在问题转化为求后面的每一个条件概率。

但其实你会发现，这些条件概率非常不好求，因为这个数据简直没法计算。

特别是约到后边，条件概率对应的先验概率就会越复杂。

存在两个致命的缺陷：

• 参数空间过大，不可能实用化
• 数据稀疏严重

n-Gram

1-Gram

利用马尔科夫链的假设

我们做一个假设，第n个词出现的概率只与钱n-1个词有关系。

极端一些，先把n取1，也就是每个词的出现都是独立的。

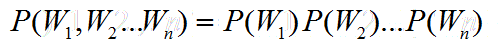
2-Gram

假设n取2，也就是每个词的出现仅与前一个词出现有关。

此时为2-Gram模型也就是Bi-Gram，句子的概率为：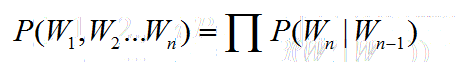

3-Gram

假设n取3，也就是每个词的出现仅与前两个词有关，此时为3-Gram模型，也就是Tr-Gram，句子的概率为：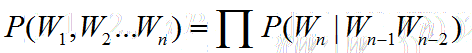

回到我们刚刚那句话，今天天气真好，如果采用2-Gram的模型我们有：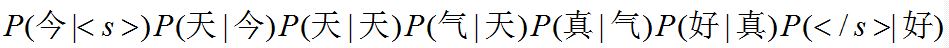

这里说明一下：采用N-Gram模型的时候，在句子开始与结束需要补充N-1个标识符。表示开始 表示结束

至此，N-Gram模型就已经基本介绍完毕了。

N-Gram 计算

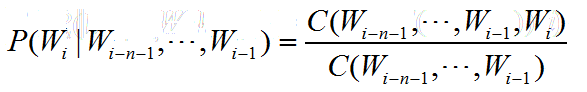
C代表的出现的次数。比方说，我们在一个语料库中已经统计好了下表。
第一行第二列代表，i出现在want前面的827次数。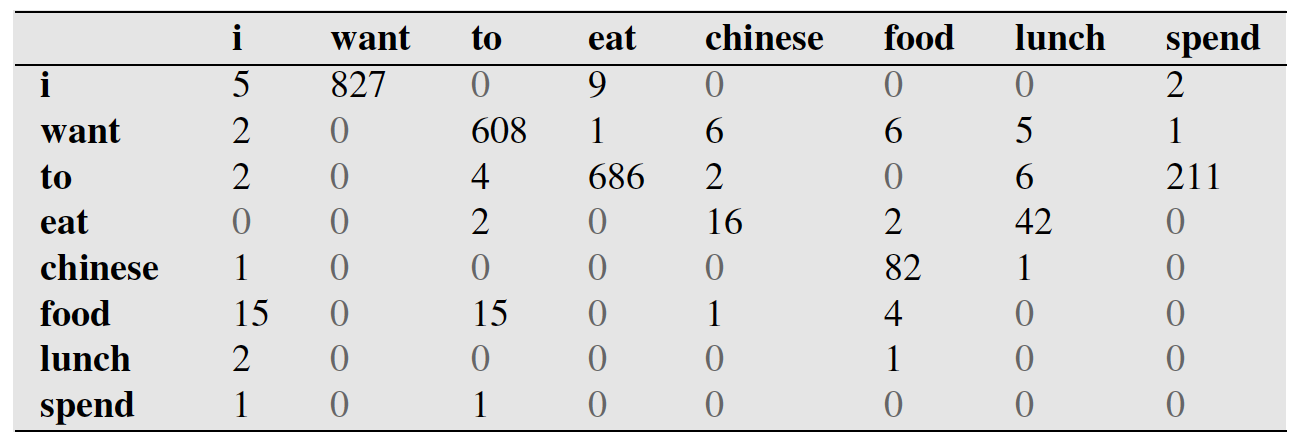

下表代表每个词出现的次数。比如i一共出现2533词。

那么概率为：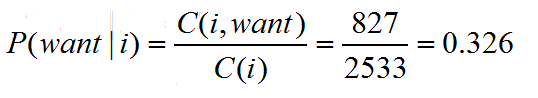

小结

无后验性在NLP中是一个很有意思的特性，在word2vec中、HMM、CRF中都有类似的特性。