矩阵分解(MF)和交替最小平方法(ALS)

矩阵分解是一种常用的推荐系统，通常研究者们只有用户-物品评分矩阵，如何从该矩阵中获得用户的个性偏好以及物品自身属性为交替最小二乘法的实现目标。

交替最小平方法(Alternating least squares, ALS)

本方法常用于基于矩阵分解的推荐系统中，如将用户-物品评分矩阵分解为两个低纬的矩阵，将每个用户和物品都表示为一个向量。

假设有m个用户和n个物品，设评分矩阵为R，矩阵分解的目标时候找到两个低维矩阵（X和Y）来逼近评分矩阵R：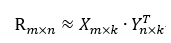

对应的解释如下：

$r_{ij}$表示用户i对物品j的评分情况，为了能让X和Y的乘积尽量的接近R，这里使用到了最小损失函数。同时损失项一般需要加入正则项以避免过拟合问题，通常使用L2正则，因此目标函数为：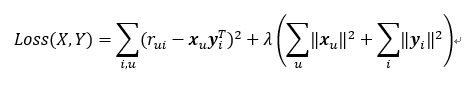

$\lambda$为正则化系数，防止过拟合用。
交替最小平方法（ALS）使用上述的平方误差，交替降低误差。何为交替降低误差呢，在每轮迭代中，只迭代其中一个参数，下回迭代另外一个参数，交替进行。

• 固定Y，对Loss做X偏微分，使其偏微分等于0：
  

• 然后固定X，对Loss做Y偏微分，使其偏微分等于0：
  

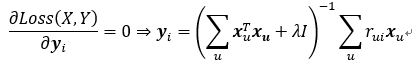
• 循环上述过程，不断交替进行，直至误差收敛为止。

具体偏微分过程

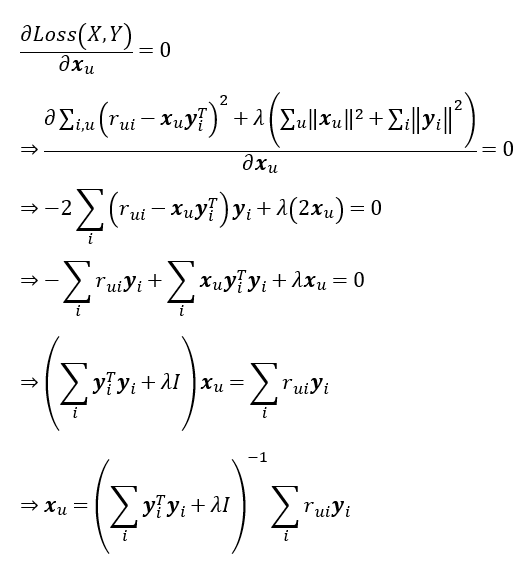
其它

• 损失函数的主体部分和正则部分，可以同一添加$\frac12$，因为求偏微分的时候右上角的2会掉下来。
• 优化方法有两种，一种是令$\frac{\partial L}{\partial x_u}=0$，得到$x_u$的值。另外一种是：$X_u \gets X_u -\gamma_x \frac{\partial L}{\partial X_u}$