Coursera ML(10)-机器学习诊断法
假设你在开发一个机器学习系统,或者在改进一个机器学习系统的性能,应如何做?
目前已有的方法:
- Getting more training examples
- Trying smaller sets of features
- Trying additional features
- Trying polynomial features
- Increasing or decreasing λ
每种方法都有自己不同的应用场景
Evaluating a Hypothesis
根据测试集得到参数,对训练集运用模型。有两种误差计算方法
For linear regression:
For classification :
误分类的比例,对于每一个测试实例,计算:然后急死俺平均
Model Selection and Train/Validation/Test Sets(交叉验证机)
使用60%的数据作为训练集,20%的数据作为交叉验证集,20%的数据作为测试集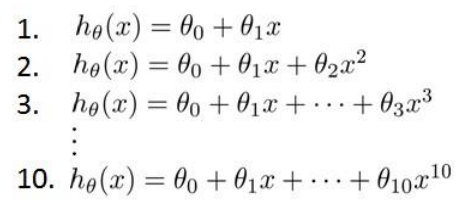
- Optimize the parameters in Θ using the training set for each polynomial degree.
- Find the polynomial degree d with the least error using the cross validation set.
- Estimate the generalization error using the test set with $J_{test}(\Theta^{(d)})$, (d = theta from polynomial with lower error);
简单来讲:
训练集训练出 10 个模型 ->10 个模型分别对交叉验证集计算得出交叉验证误差(代价函数的值)->选取代价函数值最小的模型->用选出的模型对测试集计算得出推广误差(代价函数的值)
Diagnosing Bias vs. Variance
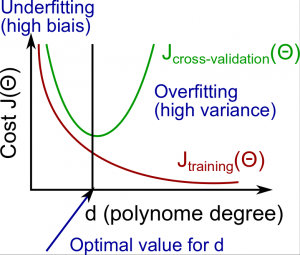
- High bias (underfitting): both $J{train}(\Theta)$ and $J{CV}(\Theta)$ will be high. Also, $J{CV}(\Theta) \approx J{train}(\Theta)$.
- High variance (overfitting): $J{train}(\Theta)$ will be low and $J{CV}(\Theta)$ will be much greater than $J_{train}(\Theta)$.
很多情况下,欠拟合会导致高误差,高方差意味着拟合过度。
Decide Bias or Variance
- 训练集误差和交叉验证集误差近似时:偏差/欠拟合
- 交叉训练集误差 >> 训练集误差时:方法/过拟合
Regularization and Bias/Variance

- Create a list of lambdas (i.e. λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24});
- Create a set of models with different degrees or any other variants.
- Iterate through the $\lambda$s and for each $\lambda$ go through all the models to learn some $\Theta$.
- Compute the cross validation error using the learned Θ (computed with λ) on the $J_{CV}(\Theta)$ without regularization or λ = 0.
- Select the best combo that produces the lowest error on the cross validation set.
- Using the best combo Θ and λ, apply it on $J_{test}(\Theta)$ to see if it has a good generalization of the problem.
简单说:
训练12个不同归一化的模型->分别对应交叉验证集计算误差->选出最小的那个->使用在测试集上Regularization 相关结论

- 当$\lambda$较小时,训练集误差较小(过拟合)而交叉验证集误差较大。
- 随着$\lambda$增加,训练集误差不断增加(欠拟合),而交叉验证集误差则是先减小后增大。
Learning Curves
- 学习曲线是一个很好的工具,我们会经常使用学习曲线来判断某一个学习算法是否处于偏差、方差问题。
- 学习曲线试讲训练集误差和交叉验证集误差作为训练集实例数量(m)的函数绘制的图表。
Experiencing high bias:
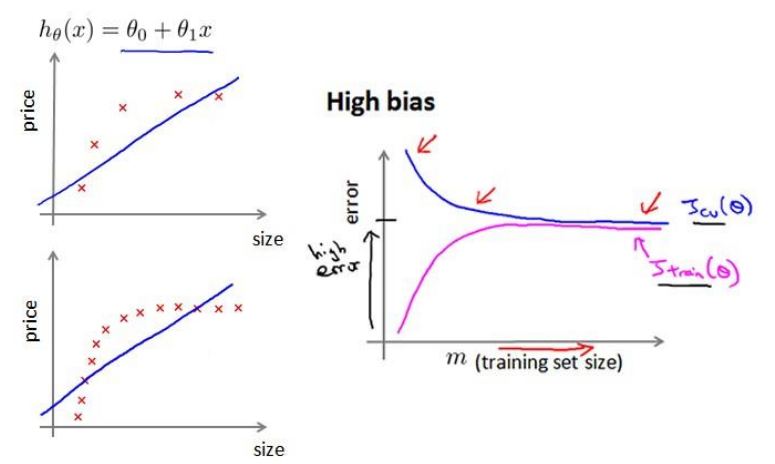
- Low training set size: causes $J{train}(\Theta)$ to be low and $J{CV}(\Theta)$ to be high.
- Large training set size: causes both $J{train}(\Theta)$ and $J{CV}(\Theta)$ to be high with $J{train}(\Theta)$≈$J{CV}(\Theta)$
因此在高偏差(欠拟合)的情况下,增加训练集数量并不是一个好办法。此时,我们应当增加features。Experiencing high variance:

- Low training set size: $J{train}(\Theta)$ will be low and $J{CV}(\Theta)$ will be high.
- Large training set size: $J{train}(\Theta)$ increases with training set size and $J{CV}(\Theta)$ continues to decrease without leveling off. Also, $J{train}(\Theta)$ < $J{CV}(\Theta)$ but the difference between them remains significant.
对比之下,如果在高方差(过拟合)的情况下,增加训练集数量可以明显降低误差,提高算法效果。
决定下一步做什么
- 获得更多的训练实例——解决高方差

- 尝试减少特征的数量——解决高方差
- 尝试获得更多的特征——解决高偏差
- 尝试增加多项式特征——解决高偏差

- 尝试减少归一化程度 λ—->提高拟合准确度—->解决高偏差
- 尝试增加归一化程度 λ—->防止过拟合—->解决高方差
Coursera ML(10)-机器学习诊断法