Coursera ML(5)-Logistic Regression and Regularization with Python

线性回归算法，可用于房屋价格的估计及股票市场分析。 Logistic Regression （逻辑回归）是当前业界比较常用的机器学习方法，用于估计某种事物的可能性。比如某用户购买某商品的可能性，某病人患有某种疾病的可能性，以及某广告被用户点击的可能性等。相关公式推导在这里

---

Stanford coursera Andrew Ng 机器学习课程编程作业（Exercise 2），作业下载链接貌似被墙了，下载链接放这。http://home.ustc.edu.cn/~mmmwhy/machine-learning-ex2.zip

预备知识

这里应该分为 正常、过拟合和欠拟合，三种情况。

• Cost Function $$J(\theta) = - \frac{1}{m} \sum_{i=1}^m \large[ y^{(i)}\ \log (h_\theta (x^{(i)})) + (1 - y^{(i)})\ \log (1 - h_\theta(x^{(i)}))\large] + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2$$

• Gradient Descent

  $$\begin{align*} & \text{Repeat}\ \lbrace \newline & \ \ \ \ \theta_0 := \theta_0 - \alpha\ \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_0^{(i)} \newline & \ \ \ \ \theta_j := \theta_j - \alpha\ \left[ \left( \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} \right) + \frac{\lambda}{m}\theta_j \right] &\ \ \ \ \ \ \ \ \ \ j \in \lbrace 1,2...n\rbrace\newline & \rbrace \end{align*}$$

• Grad

  $$Grad = \frac{1}{m}\ \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}+ \frac{\lambda}{m}\theta_j$$

后边有一个$\frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2$和$\frac{\lambda}{m}\theta_j$小尾巴，作用就是进行 Regularization，防止拟合过度。

Logistic Regression

题目介绍

• you will build a logistic regression model to predict whether a student gets admitted into a university.（根据各科目分数预测该学生是否能录取）
• For each training example, you have the applicant’s scores on two exams and the admissions decision.
• Your task is to build a classication model that estimates an applicant’s probability of admission based the scores from those two exams.

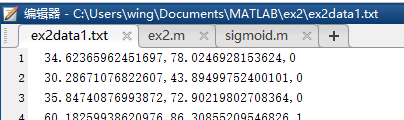
python code

from numpy import *
import matplotlib.pyplot as plt
from scipy import optimize

def init(path):
    X,y = load_dataset(path) # 调用底下那个东西
    m, n = shape(X)
    initial_theta = zeros(n + 1)
    return X,y,m,n,initial_theta
    
def load_dataset(path):
    data = loadtxt(path, delimiter=',')
    X = data[:,:2]
    y = data[:, 2]
    return X,y

def plotData(X,y):
    plt.plot(X[y==1][:,0],X[y==1][:,1],'k+',linewidth=2,)
    plt.plot(X[y==0][:,0],X[y==0][:,1],'ko',color='y',linewidth=2)
    plt.xlabel('科目一成绩', fontproperties='SimHei')
    plt.ylabel('科目二成绩', fontproperties='SimHei')
    plt.title('分数与录取的关系', fontproperties='SimHei')
    
    
def sigmoid(X, theta):
    return 1 / (1 + exp(-dot(X, theta)))

def get_cost(theta, X, y):
    J = sum((-y*log(sigmoid(X,theta)) - (1-y)*log(1-sigmoid(X,theta))))/len(X)
    return J

def get_grad(theta, X, y):
    return (sigmoid(X,theta) - mat(y))*X*(1/m)

def plotDecisionBoundary(theta, X, y):
    plotData(X[:, 1:3], y)
    if X.shape[1] <= 3:
        plot_x = r_[X[:,2].min()-2,  X[:,2].max()+2]
        plot_y = - (theta[1]*plot_x + theta[0])/theta[2]
        plt.plot(plot_x, plot_y)
        plt.axis([30,100,30,100])
        plt.legend(['Accepted', 'Not Accepted', 'Decision Boundary'])
        plt.show()
    else:
        pass

    
def predict(theta, X):  
    prob = sigmoid([1,45,85] , result[0])
    return prob
    
if __name__=="__main__":
    path = 'C:\\Users\\wing\\Desktop\\machine-learning-ex2\\ex2\\ex2data1.txt'
    X,y,m,n,initial_theta = init(path)
    X = column_stack((ones(m), X))
    cost = get_cost(initial_theta, X, y)
    grad = get_grad(initial_theta, X, y)

    # obtain the optimal theta
    result = optimize.fmin_tnc(func=get_cost, x0=initial_theta, fprime=get_grad, args=(X, y))  
    get_cost(result[0], X, y)  
    # result = (array([-25.16131863,   0.20623159,   0.20147149]), 36, 0)
    # get_cost(result[0], X, y)  = 0.20349770158947464
    plotDecisionBoundary(result[0], X, y)
    print('For a student with scores 45 and 85, we predict an admission ' \
         'probability of %f\n'%predict(result[0], X))

# For a student with scores 45 and 85, we predict an admission probability of 0.776291

运行结果

最后进行了一个测试，如果一个学生两门考试成绩，一门45分，另外一门85分，那么他被录取的概率为77%。幸亏是在外国，在中国这分数，连大专都考不上。

Logistic Regression and Regularization

题目

• Suppose you are the product manager of the factory and you have the test results for some microchips on two dierent tests.
• 对于一批产品，有两个检测环节，通过检测结果判断产品是否合格。比如，宜家会有三十年床垫保证，那么如果确保床垫合格（用30年），我们只能通过一些检测，来推测产品是否合格。

python code

from numpy import *
import matplotlib.pyplot as plt
from scipy import optimize

def init(path):
    X,y = load_dataset(path)
    dataplot(X,y)
    X = map_feature(X[:,0], X[:,1])
    initial_theta = zeros(size(X[1]))
    lam = 1
    return X,y,initial_theta,lam

def load_dataset(path):
    data = loadtxt(path, delimiter=',')
    X = data[:,:2]
    y = data[:, 2]
    return X,y
    
def dataplot(X,y):
    plt.plot(X[y==1][:,0],X[y==1][:,1],'k+',linewidth=2)
    plt.plot(X[y==0][:,0],X[y==0][:,1],'ko',color='y',linewidth=2)
    plt.legend([ 'y = 1','y = 0'])

def sigmoid(X, theta):
    return 1 / (1 + exp(-dot(X, theta)))


def map_feature(x1, x2):
    #X1, X2, X1 ** 2, X2 ** 2, X1*X2, X1*X2 ** 2, etc...

    x1.shape = (x1.size, 1)
    x2.shape = (x2.size, 1)
    degree = 6
    out = ones(shape=(x1[:, 0].size, 1))
    m, n = out.shape
    for i in range(1, degree + 1):
        for j in range(i + 1):
            r = (x1 ** (i - j)) * (x2 ** j)
            out = append(out, r, axis=1)
    return out

def get_cost(theta, X, y,lam):
    hx = sigmoid(X,theta)
    thetaR = theta[1:]
    J = sum((-y*log(hx) - (1-y)*log(1-hx)))/len(X) \
        + (lam / (2.0 * len(X))) * (thetaR.T.dot(thetaR))
    return J

def get_grad(theta, X, y,lam):
    reg = (lam/len(y))*theta
    reg[0] = 0
    grad = X.T.dot(sigmoid(X,theta)-y)/len(y)+reg
    return grad

def plotDecisionBoundary(theta,lam):
    u = linspace(-1, 1.5, 50)
    v = linspace(-1, 1.5, 50)
    z = zeros(shape=(len(u), len(v)))
    for i in range(len(u)):
        for j in range(len(v)):
            z[i, j] = (map_feature(array(u[i]), array(v[j])).dot(array(theta)))
    z = z.T
    plt.contour(u, v, z)
    plt.title('lambda = %f' % lam)
    plt.xlabel('Microchip Test 1')
    plt.ylabel('Microchip Test 2')
    plt.axis([-0.85,1.1,-0.85,1.1])
    plt.legend(['y = 1', 'y = 0', 'Decision boundary'])
    plt.show()
    
if __name__=="__main__":
    path = 'C:\\Users\\wing\\Desktop\\machine-learning-ex2\\ex2\\ex2data2.txt'
    X,y,initial_theta,lam = init(path)
    result = optimize.fmin_tnc(func=get_cost, x0=initial_theta, fprime=get_grad, args=(X, y,lam))  
    plotDecisionBoundary(result[0],lam)

运算结果

• 过拟合
  lambda=0。不考虑$\frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2$和$\frac{\lambda}{m}\theta_j$，我们可以看到图像已经被拟合过度。这样的答案没有通用性
  
• 欠拟合
  lambda=10，欠拟合会导致数据的很多细节被抛弃。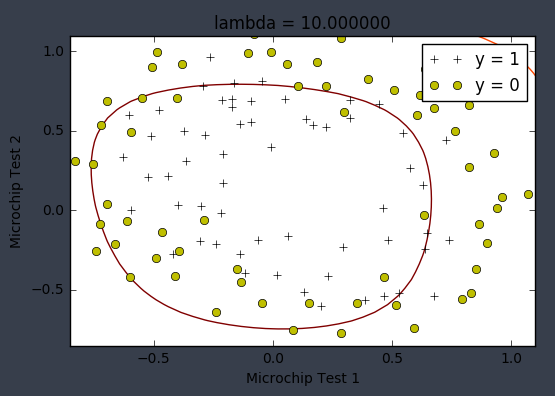
  
• 拟合较好
  lambda=1，准确性到91%左右，这个准确率算低的了吧，还有很大上升空间。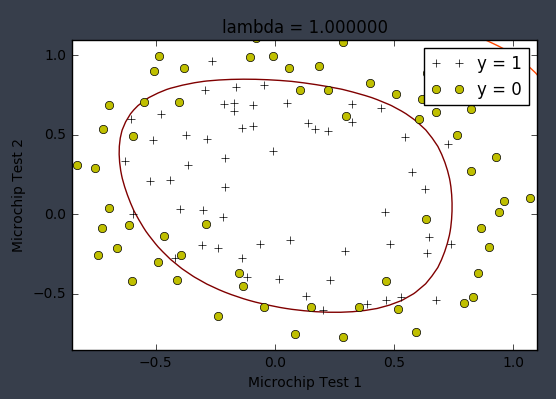
  

Summary

熊辉上课的时候，说机器学习需要调参数，参数很不好调，需要使用者对数据有极高的敏感度。

参数lambda就是这种感觉，感觉真的是乱调一通，然后就发现，诶哟，好像还不错。

参考链接：
scipy.optimize.minimize
Logistic regression
Machine Learning Exercises In Python, Part 3
machine-learning-with-python-logistic

---

以上