长短时记忆网络 LSTM
由于RNN也有梯度消失的问题,因此很难处理长序列的数据,大牛们对RNN做了改进,得到了RNN的特例LSTM(Long Short-Term Memory),它可以避免常规RNN的梯度消失,因此在工业界得到了广泛的应用。
在RNN模型里,我们讲到了RNN具有如下的结构,每个序列索引位置t都有一个隐藏状态$h^{(t)}$。
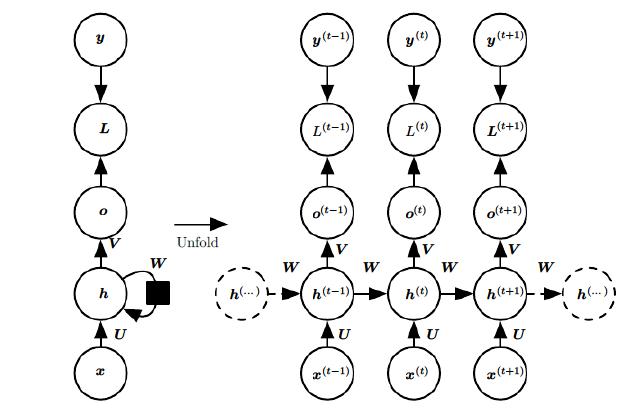
如果我们略去每层都有的$o^{(t)}$,$L^{(t)}$,$y^{(t)}$,则RNN的模型可以简化成如下图的形式:
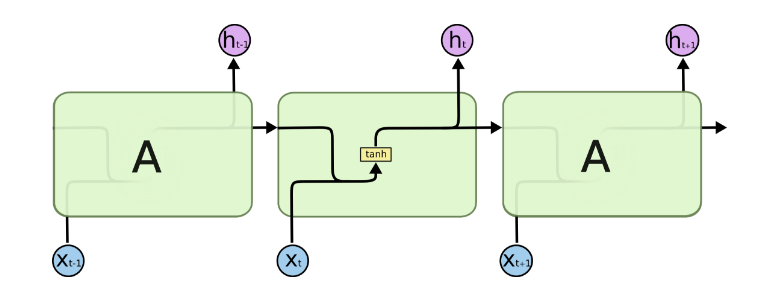
图中可以很清晰看出在隐藏状态$h^{(t)}$由$x^{(t)}$和$h^{(t−1)}$得到。得到$h^{(t)}$后一方面用于当前层的模型损失计算,另一方面用于计算下一层的$h^{(t+1)}$。
由于RNN梯度消失的问题,大牛们对于序列索引位置t的隐藏结构做了改进,可以说通过一些技巧让隐藏结构复杂了起来,来避免梯度消失的问题,这样的特殊RNN就是我们的LSTM。由于LSTM有很多的变种,这里我们以最常见的LSTM为例讲述。LSTM的结构如下图:
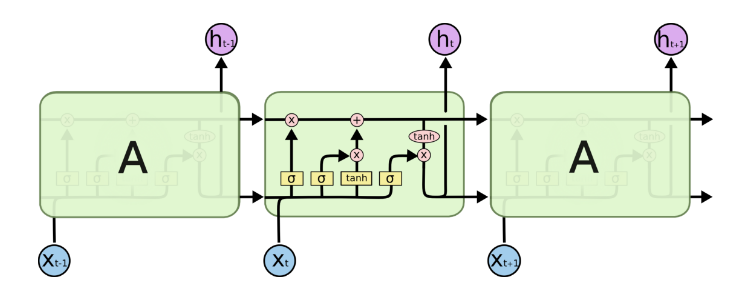
LSTM模型结构剖析
上面我们给出了LSTM的模型结构,下面我们就一点点的剖析LSTM模型在每个序列索引位置t时刻的内部结构。
从上图中可以看出,在每个序列索引位置t时刻向前传播的除了和RNN一样的隐藏状态$h^{(t)}$,还多了另一个隐藏状态,如图中上面的长横线。这个隐藏状态我们一般称为细胞状态(Cell State),记为$C^{(t)}$。如下图所示:
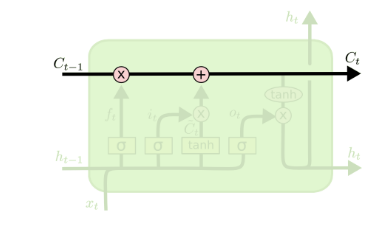
除了细胞状态,LSTM图中还有了很多奇怪的结构,这些结构一般称之为门控结构(Gate)。LSTM在在每个序列索引位置t的门一般包括遗忘门,输入门和输出门三种。下面我们就来研究上图中LSTM的遗忘门,输入门和输出门以及细胞状态。
LSTM之遗忘门
遗忘门(forget gate)顾名思义,是控制是否遗忘的,在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态。遗忘门子结构如下图所示:
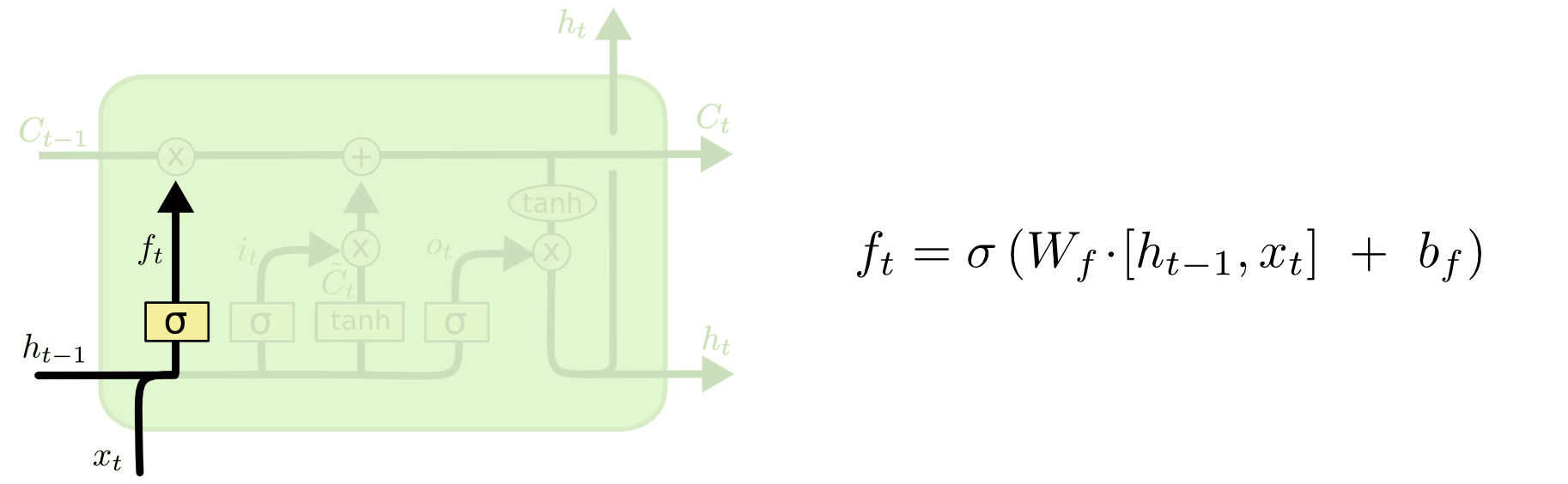
图中输入的有上一序列的隐藏状态$h^{(t−1)}$和本序列数据$x^{(t)}$,通过一个激活函数,一般是sigmoid,得到遗忘门的输出$f^{(t)}$。由于sigmoid的输出$f^{(t)}$在[0,1]之间,因此这里的输出$f^{(t)}$代表了遗忘上一层隐藏细胞状态的概率。
其中$W_f$, $b_f$为线性关系的系数和偏倚,和RNN中的类似。$\sigma$为sigmoid激活函数。
LSTM之输入门
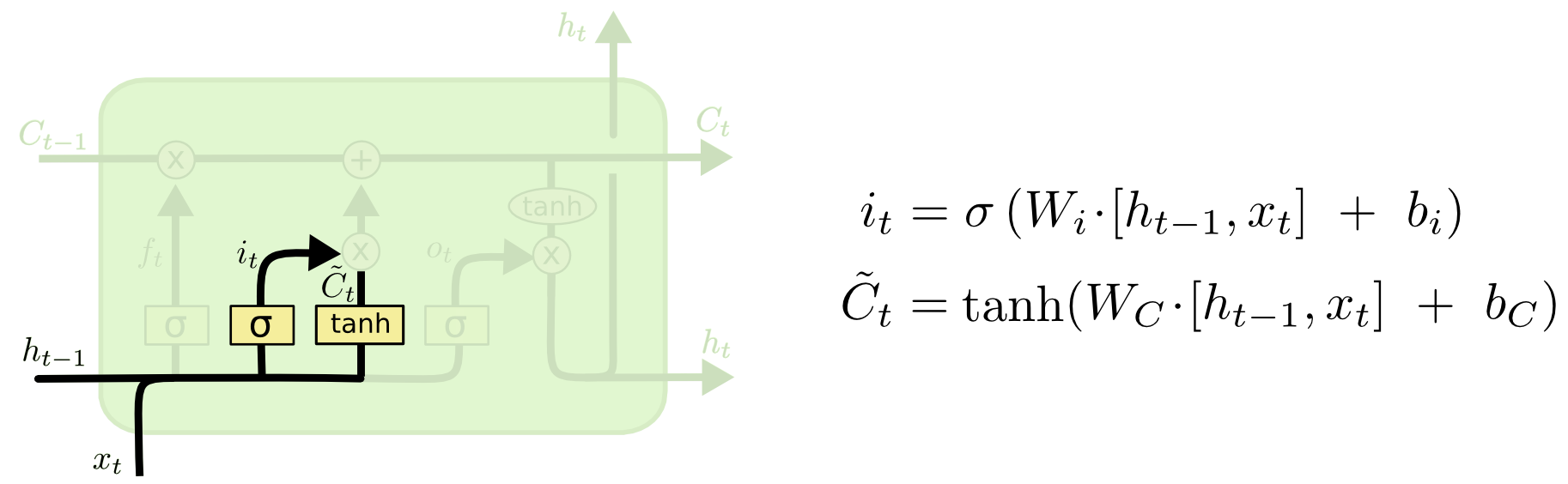
从图中可以看到输入门由两部分组成。
第一部分使用了sigmoid激活函数,输出为$i^{(t)}$。
第二部分使用了tanh激活函数,输出为$a^{(t)}$, 两者的结果后面会相乘再去更新细胞状态。
LSTM之细胞状态更新
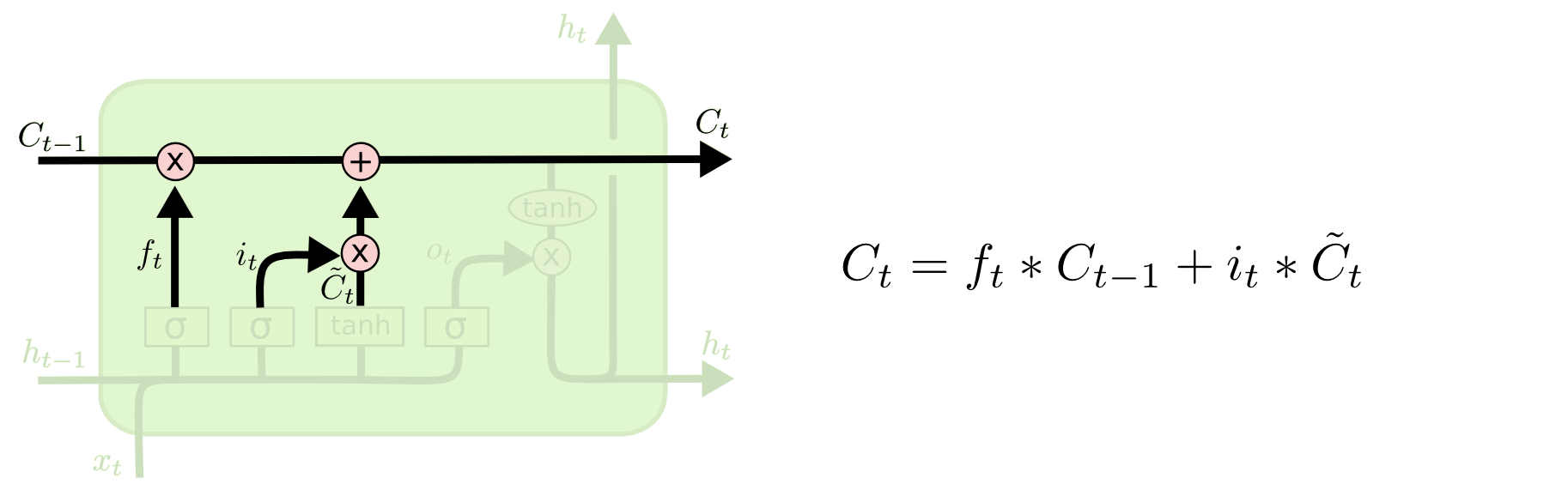
其中,⊙为Hadamard积
细胞状态$C^{(t)}$由两部分组成.
第一部分是$C^{(t−1)}$和遗忘门输出$f^{(t)}$的乘积
第二部分是输入门的$i^{(t)}$和$a^{(t)}$的乘积
LSTM之输出门
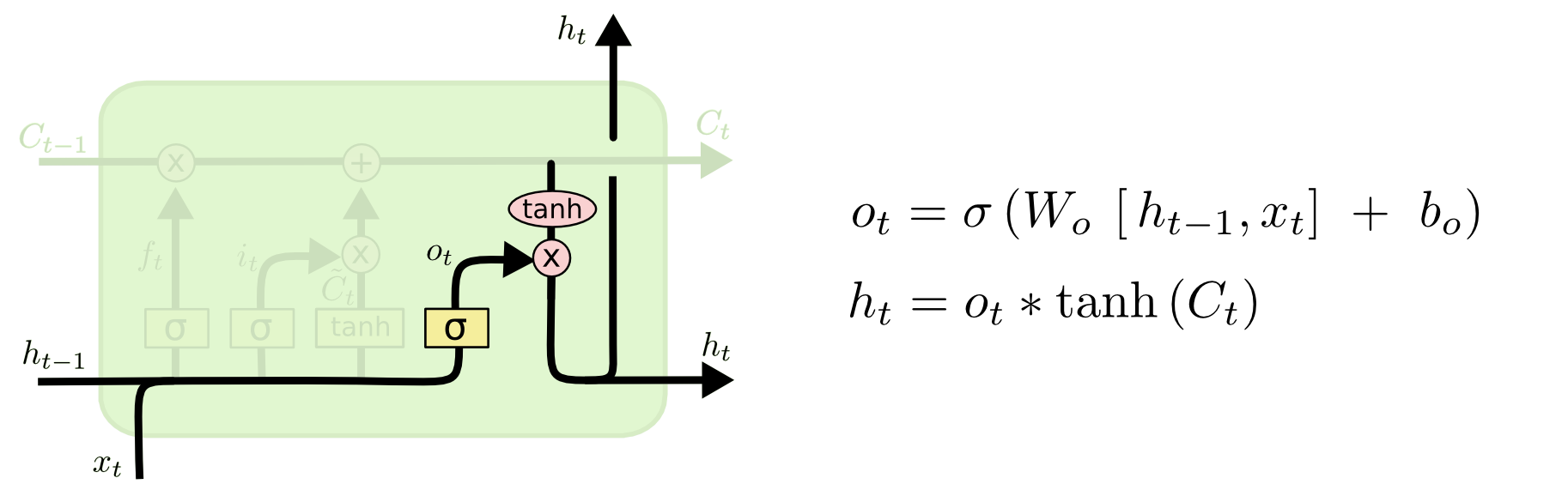
从图中可以看出,隐藏状态h(t)的更新由两部分组成
第一部分是$o^{(t)}$, 它由上一序列的隐藏状态$h^{(t−1)}$和本序列数据$x^{(t)}$,以及激活函数sigmoid得到
第二部分由隐藏状态$C^{(t)}$和tanh激活函数组成
以上就是LSTM前向传播的过程
参考
长短时记忆网络 LSTM