排序算法总结

排序算法是最常见的一种算法，生活中比较常见的实现方式有快速排序和归并排序。

归并排序

归并排序就是先把左半边数组排好序，再把右半边的数组排好序，然后进行将两侧的数组进行合并。

• 伪代码框架

理解上来说，归并排序就像是二叉树的中序遍历，排序算法很容易和二叉树联系起来。

def sort(nums, left, right):
    # left, right 边界左右均闭
    if right >= left:
        return
    mid = (left + right) // 2
    # 处理左半边的数组
    sort(nums,left,mid)
    # 处理右半边
    sort(nums,mid,right)
    merge(nums, left, mid, right)

• python 实现

from typing import List

class Solution:
    def merge_sort(self, nums, l, r):
        # 两侧都是闭合的
        if l == r:
            return
        mid = (l + r) // 2
        self.merge_sort(nums, l, mid)
        self.merge_sort(nums, mid + 1, r)
        
        result = []
        left_idx, right_idx = l, mid + 1
        while left_idx <= mid or right_idx <= r:
            if l <= left_idx <= mid < right_idx <= r:
                # 正常范围内的
                if nums[left_idx] < nums[right_idx]:
                    result.append(nums[left_idx])
                    left_idx += 1
                else:
                    result.append(nums[right_idx])
                    right_idx += 1
            elif left_idx > mid:
                # 左半边全合并了，只有右半边了
                result.append(nums[right_idx])
                right_idx += 1
            elif right_idx > r:
                # 右半边全合并了，只有左半边了
                result.append(nums[left_idx])
                left_idx += 1
        
        nums[l: r + 1] = result
    
    def sortArray(self, nums: List[int]) -> List[int]:
        self.merge_sort(nums, 0, len(nums) - 1)
        return nums

如图所示

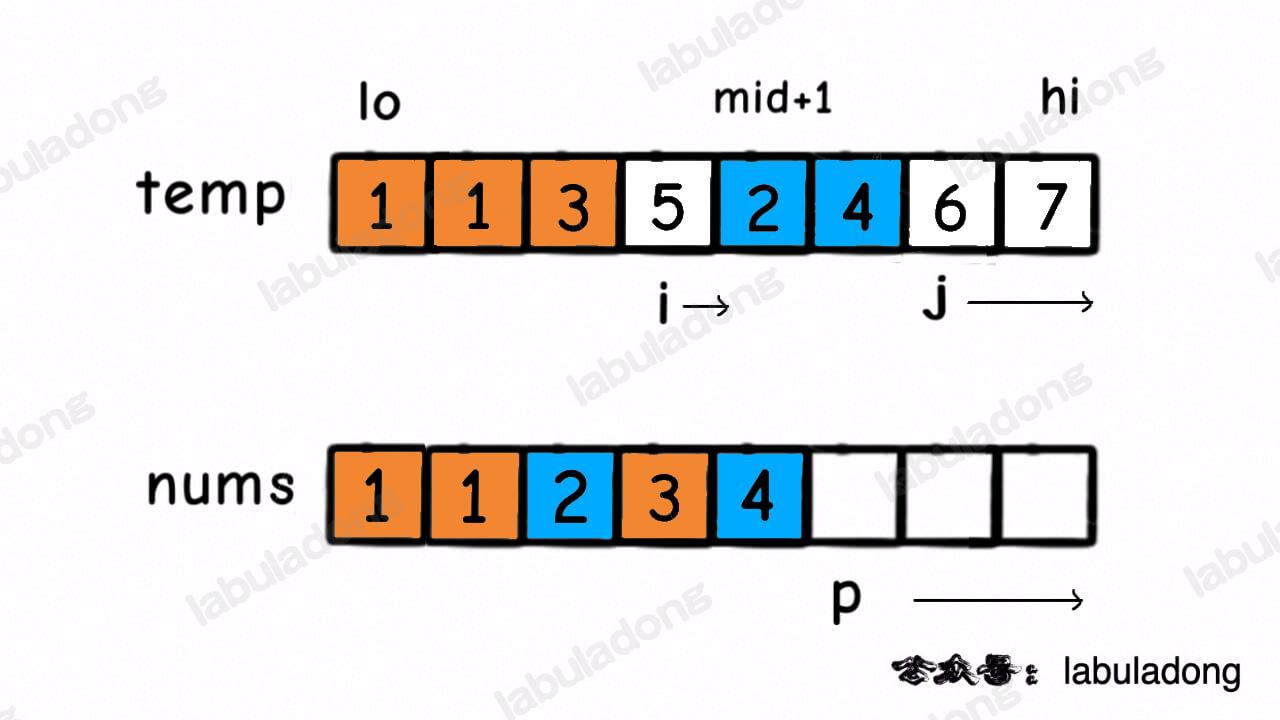
归并排序的时间复杂度是非常好的 $O(NlogN)$ ，而且不存在极端情况，分治的思想在算法中也是经常用到。

快速排序

快速排序的标准实现有两种：

• 使用最后一个元素 r 作为 povit

基本过程可以参考《算法导论》上的介绍

class Solution:
    def partition(self, nums, left, right):
        x = nums[right]
        i = left - 1
        for j in range(left, right):
            if nums[j] < x:
                i += 1
                nums[i], nums[j] = nums[j], nums[i]
        # nums[i] < nums[right]，交换后结果正确
        nums[i + 1], nums[right] = nums[right], nums[i + 1]
        return i + 1
    
    def sort(self, nums, left, right):
        if right <= left:
            return
            # 实现 left, right 范围内的排序
        p = self.partition(nums, left, right)
        self.sort(nums, left, p - 1)
        self.sort(nums, p + 1, right)
    
    def sortArray(self, nums: List[int]) -> List[int]:
        # 实现一个快速排序
        self.sort(nums, 0, len(nums) - 1)
        return nums

• 使用第一个元素作为 pivot

class Solution:
    def partition(self, nums, left, right):
        pivot = nums[left]
        i, j = left + 1, right
        while i <= j:
            while i < right and nums[i] < pivot:
                i += 1
            while j > left and nums[j] > pivot:
                j -= 1
            
            # 避免已经错过了还交换
            if i >= j:
                break
            
            nums[i], nums[j] = nums[j], nums[i]
        # 最后将 pivot 放到该放的位置上
        # 此时要么 i==j，那么无所谓
        # 要么 j < i，那么 nums[j] < nums[i]， 且 nums[j] < nums[left]
        # 交换后结果依然是正确的
        nums[left], nums[j] = nums[j], nums[left]
        return j
    
    def sort(self, nums, left, right):
        if right <= left:
            return
            # 实现 left, right 范围内的排序
        p = self.partition(nums, left, right)
        self.sort(nums, left, p - 1)
        self.sort(nums, p + 1, right)
    
    def sortArray(self, nums: List[int]) -> List[int]:
        # 实现一个快速排序
        random.shuffle(nums)
        self.sort(nums, 0, len(nums) - 1)
        return nums

悲剧的是，这两种快排实现都不能满足912. 排序数组的耗时要求…..

第 k 大的元素

对于第 k 大的元素，可以理解为从大到小排序中的第 k -1 的元素

或者从小到大排序中的第 n - k 的元素。

from typing import List


# leetcode submit region begin(Prohibit modification and deletion)
class Solution:
    def partition(self, nums, left, right):
        pivot = nums[right]
        i = left - 1
        for j in range(left, right):
            # 注意 nums[j] > pivot: 决定了是从大到小排序
            if nums[j] > pivot:
                i += 1
                nums[i], nums[j] = nums[j], nums[i]
        nums[i + 1], nums[right] = nums[right], nums[i + 1]
        return i + 1
    
    def findKthLargest(self, nums: List[int], k: int) -> int:
        k_1 = k - 1
        left, right = 0, len(nums) - 1
        
        while left <= right:
            pos = self.partition(nums, left, right)
            if pos < k_1:
                left = pos + 1
            elif pos > k_1:
                right = pos - 1
            else:
                return nums[pos]


# leetcode submit region end(Prohibit modification and deletion)


if __name__ == "__main__":
    solution = Solution()
    print(solution.findKthLargest([3, 2, 1, 5, 6, 4], 2))
    print(solution.findKthLargest([3, 2, 3, 1, 2, 4, 5, 5, 6], 4))
    print(solution.findKthLargest([1], 1))

partition 返回的位置 pos ，我们都知道其左边数组均小于 nums[pos]，右边数组均大于 nums[pos] 。

对比 pos 与 k 的大小:

• 如果 pos < k : 说明第 k 个位置上的元素，在 pos 的右侧；
• 如果 pos > k : 说明第 k 个位置上的元素，在 pos 的左侧；
• 如果 pos == k: 返回结果