面试题62. 圆圈中最后剩下的数字

题目

0,1,,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

示例 1：

输入: n = 5, m = 3
输出: 3


示例 2：

输入: n = 10, m = 17
输出: 2


限制：

1 <= n <= 10^5
1 <= m <= 10^6

• 每次重新数的位置，都是上次删除数字的下一位。

暴力解法

我的第一反应是，将每次的起点的记录下来，然后计算( x + m - 1 ) % len(data)

写出的代码如下：

class Solution:
    def lastRemaining(self, n: int, m: int) -> int:
        data = [i for i in range(n)]
        new_m = m - 1
        index = 0
        while(len(data) != 1):
            # 当前的位置
            index += m - 1
            index %= len(data) 

            data = data[:index] + data[index+1:]
        return data[0]

结果应该是正确的，但实际上不可用，因为循环次数过多，计算复杂。

递推解法

首先将过程进行罗列：

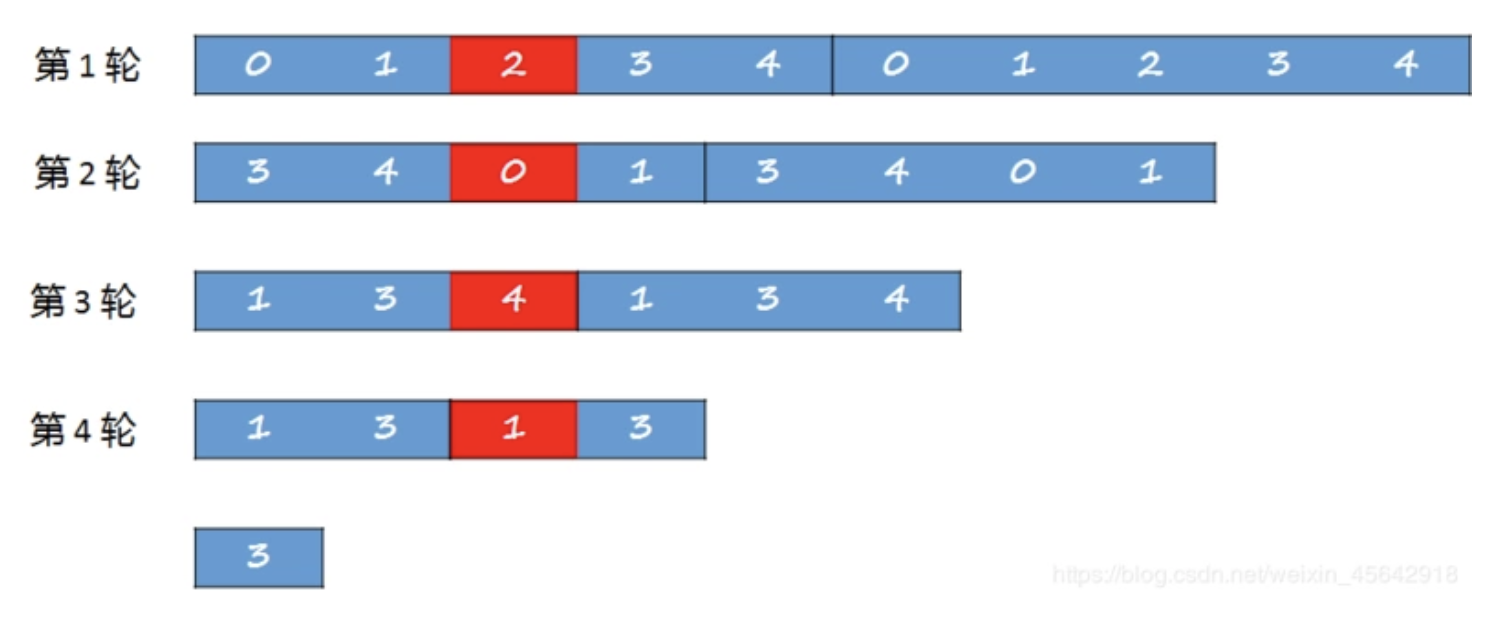
如果我们用

• f(n,m) 表示 n 个数字，每次删除第 m 个元素，最终保留下来的元素编号

• f(n-1,m) 表示 n 个数字时，每次删除第 m 个元素，最终留下来的元素编号。

问题1：如果我们知道 5 个数的时候，最终 2 会留下来。那么 4 个数字的时候，谁会留下来呢？

回答1：当第一次把 2 删除之后，所有的元素都前进了 3 位(因为重新从3开始排序的原因)。 所以4个人的时候，第 0 个位置的会留到最后。

问题2: 如果我们知道 4 个数字的时候，第0个位置的会留下来。那么 5 个数字的时候，谁会留下来？

回答2: 这是上一个问题的逆过程，所有元素向后退 3 个元素即可。因此 f(5,3) = f(4,3) + 3 ，但数组存在越界问题，因此 f(5,3) = f(4,3) + 3 % 5

于是递推公式可以为：

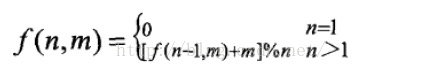
当前位置要删除的元素，应该是 (上次的起点 + m ) %当前长度得到，那么可以递推得到

• n = 1 时，要删除的元素：0；
• n = 2 时，索引：(0 + m) % 2；
• n = 3 时，索引：((0 + m) % 2 + m) % 3；
• n = 4 时，索引：(((0 + m) % 2 + m) % 3 + m) % 4；
• n = 5 时，索引：((((0 + m) % 2 + m) % 3 + m) % 4 + m) % 5。

class Solution:
    def lastRemaining(self, n: int, m: int) -> int:
        ans = 0
        # 最后 1 位为最终保留数字
        # 往前逆推，从元素个数为 2 开始
        for i in range(2, n + 1):
            # 逆推公式
            ans = (ans + m) % i
        
        return ans