Coursera ML(2)-Model and Cost Function

Model and Cost Function / Parameter Learning / Gradient Descent For Linear Regression

---

Model and Cost Function

Tables	Are
Hypothesis	$h_{\theta}={\theta}_0+{\theta}_1x$
Parameter	${\theta}_0$，${\theta}_1$
Cost Function	$J(\theta0,\theta_1)= \frac1{2m}\sum{i=1}^m(h_{\theta}(x^i)-y^i)^w$
Goal	$minimiseJ(\theta_0,\theta_1)$

Model Representation

• Hypothesis: $$h_{\theta}={\theta}_0+{\theta}_1x$$ ${\theta}_0$和${\theta}_1$称为模型参数

Cost Function

We can measure the accuracy of our hypothesis function by using a cost function. his takes an average difference (actually a fancier version of an average) of all the results of the hypothesis with inputs from x’s and the actual output y’s. 如何尽可能的将直线与我们的数据相拟合

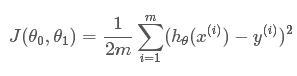
Parameter Learning

Gradient descent idea

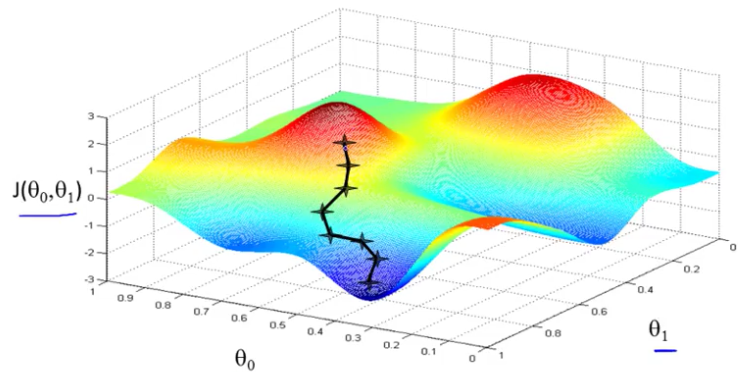
Turns out, that if you’re standing at that point on the hill, you look all around and you find that the best direction is to take a little step downhill is roughly that direction. Okay, and now you’re at this new point on your hill. You’re gonna, again, look all around and say what direction should I step in order to take a little baby step downhill? And if you do that and take another step, you take a step in that direction.

Gradient descent algorithm

repeat until convergence:{

$$\theta_j:=\theta_j-\alpha\frac\partial{\partial\theta_j}J(\theta_0,\theta_1)$$

}

• use := to denote assignment, so it’s the assignment operator.
• $\alpha$ called:learning rate.controls how big a step we take downhill with creating descent.
• $\theta_0,\theta_1 $should be updated simultaneously(using multiple temp var should work!)
  

Gradient Descent For Linear Regression

$$\begin{align*} \text{repeat until convergence: } \lbrace & \newline \theta_0 := & \theta_0 - \alpha \frac{1}{m} \sum\limits_{i=1}^{m}(h_\theta(x_{i}) - y_{i}) \newline \theta_1 := & \theta_1 - \alpha \frac1m \sum\limits_{i=1}^m\left((h_\theta(x_i) - y_i) x_i\right) \newline \rbrace& \end{align*}$$

where m is the size of the training set, $\theta_0$ a constant that will be changing simultaneously with $\theta_1$ and $x_i y_i$are values of the given training set (data).

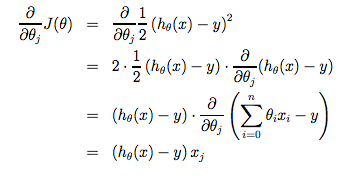
• The $J(θ_0,θ_1)$ is a convex function, which means it has only one global minimun, which means gradient descent will always hit the best fit

• “Batch” Gradient Descent: “Batch” means the algo is trained from all the samples every time