SVM(1) 之 拉格朗日乘子法和KKT条件

其实我之前看过这个地方，但是当时感触不深(或者说根本没看懂,也可能是忘了)，所以重新推导一下。

拉格朗日乘法谈起

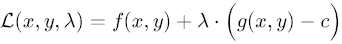
拉格朗日乘法拉格朗日乘数法是用来求条件极值的，极值问题有两类，其一，求函数在给定区间上的极值，对自变量
没有其它要求，这种极值称为无条件极值。其二，对自变量有一些附加的约束条件限制下的极值，称为
条件极值。

求这个椭球的内接长方体的最大体积。

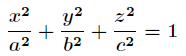
下，求

最大值。

通过拉格朗日乘数法将问题转化为

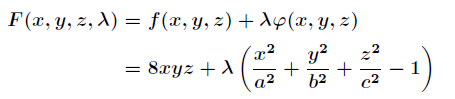
然后分别对x,y,z,兰姆达 求导，得到最值，带回原式即可

更多参考
https://zh.wikipedia.org/wiki/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E4%B9%98%E6%95%B0
https://blog.csdn.net/acdreamers/article/details/41413445

拉格朗日对偶法

《统计学习方法》 附录C

原始问题

假设$f(x), c{i}(x), h{j}(x)$是定义在R^n上的连续可微函数，考虑约束最优化问题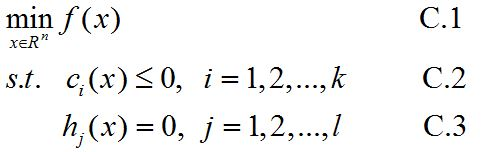

很多时候，现实问题可能跟上述结构不一样，那么把问题转化一下即可，比如 max->min

拉格朗日函数

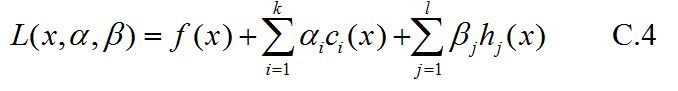
其中，$α_i β_i$ 是拉格朗日乘子，并且要求$α_i ≥ 0$。

首先我们把$L(x,α,β)$看成是$α,β$的函数（把x看成常量），然后求该函数的最大值（含x的表达式），接着再把x看成变量，因此可以定义函数$θ_p(x)$如下：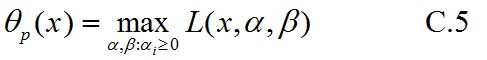

下标$P$代表原始问题

这里或许可以看到一些拉格朗日乘法的影子，最值 求导 然后带回原式。至于为什么是max而不用min，一种说法是c_i(x)<=0而 $α_i$ 没上限，所以式子可以一直小下去的，再所以用的是max。

可以证明，如果 $x$满足原始问题中约束，那么 $\theta({x})=f({x})$

为什么 $\theta(\boldsymbol{x})=f(\boldsymbol{x})$ ，这里看一下$L$ 里边的参数，$c_i(x)$小于0，$a_i$大于0，这两项乘积<=0，$h_j(x)$又都是0，那么 L的最大值 其实 就只有一个 f(x) 了，毕竟别的都是负数。

如果 $x$不满足原始问题中的约束$c_i(x)\le 0;h_j(x)=0$，那么$\theta(\boldsymbol{x})=+\infty$，即：

所以如果考虑极小化问题：

$$\min_{\boldsymbol{x} }f(\boldsymbol{x})=\min_{\boldsymbol{x} }\theta_P(\boldsymbol{x})=\min_{\boldsymbol{x} }\max_{\boldsymbol{\alpha,\beta}:\alpha_i\ge0}L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta})$$

$\min{\boldsymbol{x} }\max{\boldsymbol{\alpha,\beta}:\alpha_i\ge0}L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta})$ 称为广义勒格朗日函数的极小极大问题。此时原始最优化问题，转化为广义拉格朗日函数的极大极小问题。这样一来，就把原始最优化问题表示为广义拉格朗日函数的极小极大问题。我们定义原始问题最优解：

$$p^*=\min_{x}\theta_P(x)$$

• 所以这一部分到底干了什么事？

从原始问题开始，通过拉格朗日函数重新定义一个无约束问题，这个无约束问题等价于原来的约束优化问题，从而将约束问题无约束化。也就是将d个变量和k个约束条件的最优化问题转换为d+k个变量的最优化问题。到此我们还是无法求解，我们需要将原始问题转换成对偶问题来求解。

对偶问题

我们再定义：

$$\theta_D(\alpha,\beta)=\min_x L(x,\alpha,\beta)$$

并极大化$\theta_D$，即：

$$\max_{\alpha,\beta}\theta_D(\alpha,\beta)=\max_{\boldsymbol{\alpha,\beta} }\min_{\boldsymbol{x} }L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta})$$

$\max{\boldsymbol{\alpha,\beta} }\min{\boldsymbol{x} }L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta})$为广义拉格朗日函数的极大极小问题(上一节的是极小极大问题)。这样可以将广义拉格朗日函数的极大极小问题进一步表示为约束最优化问题：

$$\max_{\alpha,\beta}\theta_D(\alpha,\beta)= \max_{\boldsymbol{\alpha,\beta} }\min_{\boldsymbol{x} }L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta}) \ \ \mathbb{s.t.}\quad\alpha_i\ge0,\quad i=1,2,\cdots,k$$

对比原始问题，对偶问题是先固定$\alpha,\beta$，求最优化$x$的解，在确定参数$\alpha,\beta$；
原始问题是先固定x，求最优化$\alpha,\beta$的解，再确定$x$。

原始问题和对偶问题的关系

这块我就不证明了，书上都有。

总之，当原始问题和对偶问题的最优值相等：$d^=p^$ 时，可以用求解对偶问题来求解原始问题（当然是对偶问题求解比直接求解原始问题简单的情况下），但是到底满足什么样的条件才能使 $d^=p^$ 呢，这就是下面要阐述的 KKT 条件。

KKT 条件

作为对比，把拉格朗日函数再拿出来对比一下

$$L(\boldsymbol{x},\boldsymbol{\alpha},\boldsymbol{\beta})=f(\boldsymbol{x})+\sum_{i=1}^k \alpha_ic_i(\boldsymbol{x}) + \sum_{j=1}^l\beta_jh_j(\boldsymbol{x})$$

*	KKT条件	说明
1	$\nabla_\boldsymbol{x}L(\boldsymbol{x}^,\boldsymbol{\alpha}^,\boldsymbol{\beta}^*)=0$
2	$\nabla_\boldsymbol{\alpha}L(\boldsymbol{x}^,\boldsymbol{\alpha}^,\boldsymbol{\beta}^*)=0$
3	$\nabla_\boldsymbol{\beta}L(\boldsymbol{x}^,\boldsymbol{\alpha}^,\boldsymbol{\beta}^*)=0$	极值部分，求导为0
4	$c_i(\boldsymbol{x}^*)\le0,\quad i=1,2,\cdots,k$	C.2不等式约束
5	$h_j(\boldsymbol{x}^*)=0,\quad j=1,2,\cdots,l$	C.3等式约束
6	$\alpha_i^*\ge0,\quad i=1,2,\cdots,k$	拉格朗日算子 法线方向相反的解释
7	$\alpha_i^c_i(\boldsymbol{x}^)=0,\quad i=1,2,\cdots,k$	1、$\alpha_i^=0$ 时， $c_i(\boldsymbol{x}^)\le0$
7		2、$\alpha_i^>0$ 时， $c_i(\boldsymbol{x}^)=0$

KKT条件可以分为三部分来考虑：

• 原始拉格朗日函数求导为0
• 原始不等式条件
• 拉格朗日算子条件以及对偶互补条件